DHHS (NIOSH) Publication No. 2015–105
March 2015

This document is in the public domain and may be freely copied or reprinted.

Disclaimer

Mention of any company or product does not constitute endorsement by the National Institute for Occupational Safety and Health (NIOSH). In addition, citations to Web sites external to NIOSH do not constitute NIOSH endorsement of the sponsoring organizations or their programs or products. Furthermore, NIOSH is not responsible for the content of these Web sites. All Web addresses referenced in this document were accessible as of the publication date.

Ordering information

To receive documents or more information about occupational safety and health topics, contact NIOSH:

Telephone: 1-800-CDC-INFO (1-800-232-4636)
TTY: 1-888-232-6348
CDC INFO: www.cdc.gov/info

or visit the NIOSH Web site at www.cdc.gov/niosh

For a monthly update on news at NIOSH, subscribe to NIOSH eNews by visiting www.cdc.gov/niosh/eNews.

Suggested Citation

NIOSH [2015]. Best practice engineering control guidelines to control worker exposure to respirable crystalline silica during asphalt pavement milling. Cincinnati, OH: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, DHHS (NIOSH) Publication No. 2015–105.

Contents

• Executive Summary
• Authors and Acknowledgments
• The Silica/Asphalt Milling Machine Partnership
• Silica in Construction – Asphalt Pavement Milling
• Guidelines for Dust Control on Asphalt Milling Machines
  • Ventilation Control Guidelines for Pavement-Milling Machines
  • Water Spray Application Guidelines for Asphalt Milling Machines
• NIOSH Recommended Best Practice Test Guidance for Dust Controls on Milling Machines
• Recommendations for Operation and Maintenance of Dust Control Systems
• Silica and Health Effects
• Occupational Exposure Limits
  • Crystalline Silica Exposure Limits
• References
• Appendix A: Laboratory tracer gas test procedures to evaluate ventilation controls on asphalt pavement milling machines
• Appendix B: Field Test Procedures
• Appendix C: Explanation of Statistical Methods
• Appendix D: Use of the Spreadsheet
• Appendix E: Example Daily Dust Control Checklist
• Appendix F: NAPA/AEM Best Practice Bulletin 1/12
• Appendix G: Glossary
  

Executive Summary

This document represents more than ten years of collaborative research by labor, industry, and government to reduce respirable crystalline silica exposure during asphalt pavement milling in highway construction. The collaborative research began when the Silica/Asphalt Milling Machine Partnership was formed at the 2003 National Asphalt Pavement Association (NAPA) Annual Meeting, and studies on milling machine dust controls began later that year. The Silica/Asphalt Milling Machine Partnership is coordinated by NAPA and includes all U.S. and foreign manufacturers of heavy construction equipment that currently sell pavement-milling machines to the U.S. market. In addition to NAPA and the equipment manufacturers, the Silica/Asphalt Milling Machine Partnership includes numerous paving contractors, the International Union of Operating Engineers, the Laborers International Union of North America, the Association of Equipment Manufacturers, and government organizations including the Occupational Safety and Health Administration (OSHA), the Federal Highway Administration, and the Centers for Disease Control and Prevention’s (CDC’s) National Institute for Occupational Safety and Health (NIOSH).

Based on the research of the Silica/Asphalt Milling Machine Partnership, NIOSH recommend engineering controls that include ventilation controls in addition to water-sprays used to cool the cutting teeth. Milling machines that adopt this well-designed dust control approach have been shown to control worker exposures to respirable crystalline silica from asphalt milling operations during 21 days of personal breathing zone sampling at 11 different highway construction sites [NIOSH 2013b,c]. The 42 personal breathing zone air sampling results (21 days with 2 workers per day) were all below the NIOSH recommended exposure limit of 0.05 mg/m³ for respirable crystalline silica ranging from below the limit of detection up to 0.024 mg/m³.

NIOSH and the Silica/Asphalt Milling Machine Partnership recommend ventilation controls be placed on all new half-lane and larger asphalt milling machines to reduce worker exposure to respirable crystalline silica. It is also recommended that water-sprays be used to suppress dust on milling machines if ventilation dust controls are not available. The ventilation and water-spray dust controls described in this document represent the current knowledge of best practices developed by the Silica/Asphalt Milling Machine Partnership for controlling dust during asphalt pavement milling. This document should not limit manufacturers from implementing future improvements in dust control as new technologies or inventions become available. Manufacturers can use the procedures in Appendices A and B of this document to evaluate current and future dust controls.

Authors and Acknowledgments

The principal authors of this document were National Institute for Occupational Safety and Health (NIOSH) researchers Duane R. Hammond, Andrew B. Cecala, Jay Colinet, Alberto Garcia, Kenneth R. Mead, Alan Echt, Stanley A. Shulman, Misty J. Hein, Michael G. Gressel, Leo Michael Blade, Jeanne Zimmer, Liming Lo, Gerald J. Joy, Gregory Chekan, Ronald Kovein, and David Marlow. The document was written by NIOSH in collaboration with the National Asphalt Pavement Association, the Association of Equipment Manufacturers, the International Union of Operating Engineers, and the Laborers’ International Union of North America.

The authors thank the members of the Silica/Asphalt Milling Machine Partnership, especially the milling machine manufacturers Caterpillar Inc., Roadtec Inc., Terex Corporation, Volvo Construction Equipment, and Wirtgen America Inc., for developing engineering controls and providing their equipment for testing. The authors thank Gary Fore and Donald Elisburg for their leadership of the Partnership. The authors also thank Partnership Chair Tony Bodway and his employer Payne and Dolan Inc., Steve Henderson and his employer E&B Paving Inc., and Northeast Asphalt Inc. for their efforts on behalf of this study and for their assistance in arranging and conducting the field studies.

The authors gratefully acknowledge the contributions of the following NIOSH personnel who assisted with the technical content and review of the document: G. Scott Earnest, Ronald M. Hall, Jennifer Topmiller, Trudi McCleery, Matt Gillen, and Elizabeth Garza. The authors also thank Leonid Kopylev and his employer the Environmental Protection Agency, Kalimuthu Krishnamoorthy and his employer the University of Louisiana, William Perry and his employer the Occupational Safety and Health Administration, and Ken Hoffner and his employer the New Jersey Laborers Health and Safety Fund for their careful reviews and helpful suggestions. Milling machine illustrations were drawn by Gino Fazio of NIOSH. Cover design and document layout by Brenda Jones of NIOSH.

The Silica/Asphalt Milling Machine Partnership

The guidelines presented in this document are a result of a collaborative effort by labor, industry, and government to reduce respirable crystalline silica exposure during asphalt pavement milling in highway construction. This Silica/Asphalt Milling Machine Partnership (Partnership) is coordinated by the National Asphalt Pavement Association (NAPA) and includes all U.S. and foreign manufacturers of heavy construction equipment that currently sell pavement-milling machines to the U.S. market. In addition to NAPA and the equipment manufacturers, the Partnership includes numerous paving contractors, the International Union of Operating Engineers, the Laborers International Union of North America, the Association of Equipment Manufacturers, and government organizations including the Occupational Safety and Health Administration (OSHA), the Federal Highway Administration, and the Centers for Disease Control and Prevention’s (CDC’s) National Institute for Occupational Safety and Health (NIOSH).

Many of the partners are the same members of a previous partnership to control asphalt fume exposures during paving. The Asphalt Paving Partnership was a finalist in the 1998 Innovation in American Government Award, presented by the Ford Foundation and Harvard University’s Kennedy School of Government. The Asphalt Paving Partnership was responsible for successfully implementing engineering controls on all highway-class pavers to reduce exposure to asphalt fumes [NIOSH 1997]. The same partnership strategy is being used to implement engineering controls on pavement milling machines to reduce silica exposures. The aim of the Silica/Asphalt Milling Machine Partnership, and the focus of this document, is to identify engineering controls that could be used to reduce silica exposures among workers on half-lane and larger asphalt milling machines. The engineering controls include ventilation controls in addition to the water-spray systems used on the machines for cooling the cutting teeth. The recommendations developed in this report are based on dust control studies conducted on asphalt pavement surfaces. NIOSH and the Partnership have not evaluated the effectiveness of the best practice dust controls on other non-asphalt road surfaces such as concrete.

Five manufacturers of half-lane and larger cold-milling machines developed silica dust control strategies for their respective milling machines. NIOSH and the Partnership conducted laboratory and field studies to evaluate these controls for their effectiveness at preventing worker exposures to respirable crystalline silica. NIOSH recommend ventilation controls in addition to the water-spray systems used for cooling cutting teeth. An effective water-spray application system can also provide dust suppression at the source of dust generation on asphalt milling machines that are not fitted with ventilation controls. Ventilation controls on milling machines provided dust control capable of reducing worker exposures below the NIOSH recommended exposure limit (REL) of 0.05 mg/m³ for respirable crystalline silica. Results indicated that these engineering controls can protect workers on asphalt milling machines from silica exposures.

In April of 2002, NIOSH met with the Association of Equipment Manufacturer’s Compaction and Paving Machinery Technical Committee to propose the Silica/Asphalt Milling Machine Partnership. In June 2002, NIOSH met with representatives from NAPA, the Asphalt Institute, and the Harvard School of Public Health to propose the Silica/Asphalt Milling Machine Partnership. The Partnership was formed at the 2003 NAPA Annual Meeting, and studies on milling machine dust controls began later that year.

Milling-machine manufacturers that are Partnership members worked with research engineers from the NIOSH Division of Applied Research and Technology and the NIOSH Office of Mine Safety and Health Research to implement and test prototype dust emission-control systems based in part upon the transfer of technology from similar underground mining machinery. From 2003 to 2006, the Partnership helped facilitate six in-depth field surveys during road milling jobs. The first milling-machine field survey served as a pilot study for evaluating the effectiveness of water spray controls for a cold milling machine [NIOSH 2004]. Other field surveys provided data on the effectiveness of water spray controls for one state-of-the-art milling machine model from each of the four largest domestic manufacturers [NIOSH 2007a; 2009a,b,c].

The results of data analyses performed in 2007 suggested that improvements in engineering dust-emission controls were needed. Consequently, additional field work to evaluate the new designs also was needed. A controlled test site was located in 2008 with Silica/Asphalt Milling Machine Partnership assistance and utilized for the testing. During 2009, the data from this testing were evaluated, and two techniques were found to appreciably and statistically significantly reduce respirable dust levels in and around the milling machine [NIOSH 2011d]. These were ventilation of the cutter housing and primary conveyor areas and the addition of water sprays in the transfer area from the cutter housing to the primary conveyor loading area, with spray orientation counter to material flow. NIOSH and Partnership members concluded that further optimization of the dust emission-control systems followed by additional field testing should occur.

Another large field study was conducted in 2010 and found that the same water-spray dust-suppression controls that were tested in 2008 did not show the same reductions in respirable dust [NIOSH 2011c]. However, the ventilation control combined with water-sprays used to cool cutting teeth showed statistically significant reductions in respirable dust during both 2008 and 2010, and these results were more consistent than the results from any control that used water-spray dust suppression alone.

During 2011–2012, four laboratory tracer gas studies were conducted for four different manufacturers [NIOSH 2011a,b; 2012; 2013a]. The laboratory tracer gas studies were conducted at milling machine manufacturing facilities or milling contractor-owned facilities to determine the capture efficiency of the ventilation control before shipping the machine to a test location. The results from the laboratory studies indicated that tracer gas capture efficiencies of the evaluated ventilation controls were generally greater than 90%.

Although the earlier Silica/Asphalt Milling Machine Partnership studies did not show consistent reductions in respirable dust concentrations using only water-spray systems, one manufacturer requested additional testing of a wet drum design in 2012. The wet drum design uses gravity to release water from inside the drum through nozzles to the cutting surface to suppress dust. The results of this study showed that, while the wet drum appeared to provide increased control over the baseline water-spray configuration, the two were not statistically significantly different [NIOSH 2013d]. In addition, the magnitude of the exposure reduction did not appear to be sufficient to protect workers from excessive crystalline silica exposures. Based on the results of the wet drum evaluation and previous studies using only water-spray dust suppression, NIOSH recommended additional testing of ventilation-based controls in addition to the existing water-spray configurations.

In the summer and fall of 2012, NIOSH and the Partnership began conducting field tests of milling machines fitted with ventilation controls that had been developed by each manufacturer. The field testing consisted of full-shift personal breathing zone samples for respirable crystalline silica. Breathing zone samples were collected for the operator and the ground person who were performing the normal employee work activities of asphalt pavement milling on highway construction sites. The goal of the testing was to complete the worker exposure assessment for at least 9 days over a minimum of 3 sites for each manufacturer’s machine.

By October 2012, two manufacturers had completed the field testing with a combined 21 days of personal breathing zone sampling at 11 different highway construction sites [NIOSH 2013b,c]. The 42 personal breathing zone air sampling results (21 days with 2 workers per day) were all below the NIOSH REL of 0.05 mg/m³ for respirable crystalline silica, ranging from below the limit of detection up to 0.024 mg/m³ for the milling machines with well-designed dust controls.

Silica in Construction – Asphalt Pavement Milling

Many construction tasks have been associated with overexposure to crystalline silica [Rappaport et al. 2003]. Among these tasks are tuck pointing, concrete sawing, concrete grinding, concrete breaking, jackhammering, and abrasive blasting [NIOSH 2000; Thorpe et al. 1999; Akbar-Khanzadeh and Brillhart 2002; Glindmeyer and Hammad 1988]. Road milling has also been shown to result in overexposures to respirable crystalline silica [Linch 2002; Rappaport et al. 2003; Valiante et al. 2004]. However, the three road-milling studies do not provide enough information about the operating parameters and engineering controls present on the milling machines to determine if the overexposures were due to a lack of effective controls or poor maintenance of the machines.

A variety of machinery is employed in asphalt pavement recycling, including cold-planers, heater-planers, cold-millers, and heater-scarifiers [Public Works 1995]. Cold-milling of asphalt pavement is the focus of this document. Cold-milling, which uses a toothed, rotating cutter drum to grind and remove the pavement to be recycled, is primarily used to remove surface deterioration on both petroleum-asphalt aggregate (the focus of this document) and Portland-cement concrete road surfaces [Public Works 1995]. Key components of a typical half-lane and larger asphalt pavement milling machine are shown in Figure 1.

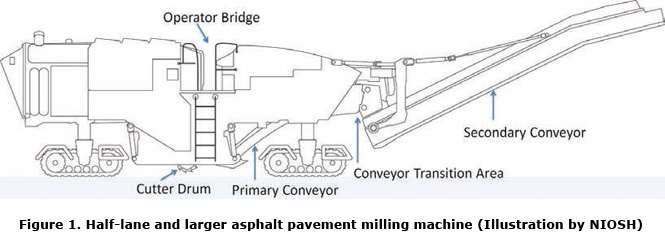
Approximately 367,000 U.S. workers are employed in highway, street, and bridge construction [U.S. Census Bureau 2007]. A number of these workers use cold-milling machines or work in close proximity to these machines. Dust generated from the cold-milling machines often contains respirable crystalline silica. This respirable dust can be transported by air currents to worker breathing zones near the milling machine.

Guidelines for Dust Control on Asphalt Milling Machines

The guidelines in this document for half-lane and larger asphalt milling machines are the result of the collaborative work of labor, industry, and government partners. The participating cold-milling machine manufacturers entered into the research project with the Partnership to reduce respirable crystalline silica exposures and improve working conditions in highway construction. The following recommendations are the result of this collaborative research partnership; ventilation recommendations are provided first, followed by guidelines for water-spray dust suppression.

Ventilation Control Guidelines for Pavement-Milling Machines

NIOSH recommends the use of ventilation controls to control worker exposures to respirable crystalline silica during asphalt pavement milling in highway construction. The ventilation controls used in combination with water-sprays that cool the cutting teeth can consistently reduce exposures below the NIOSH REL of 0.05 mg/m3 [NIOSH 2013b,c].

The ventilation controls designed to reduce respirable crystalline silica exposures on asphalt pavement milling machines should be evaluated in a controlled setting (i.e., shop or warehouse) in which their efficiency can be measured using smoke and tracer gas tests. The visible smoke test should be used as a qualitative test to visualize air-flow patterns around the milling machine drum housing and conveyors to assist in setting up for tracer gas tests. The tracer gas test should be used as a quantitative measure of the air-flow rate and capture efficiency of the ventilation system designed to control the release of respirable crystalline silica into the workers’ breathing zones. Laboratory tracer gas and smoke release test procedures to evaluate ventilation controls on asphalt pavement milling machines are provided in Appendix A.

When designing a ventilation control on a milling machine, the designer should consider the following:

• extent of enclosure around the drum housing and conveyors
• hood and duct design
• required airflow capacity
• durability and noise of the duct and fan
• measures to prevent clogging of the ventilation control

The drum housing and conveyors on the milling machine should be designed to provide maximum enclosure around the cutter drum and conveyor belts. An ideal design would have a drum housing and conveyor system that is 100% enclosed with only an opening at the top of the secondary conveyor where recycled asphalt pavement is transferred to the dump truck.

Eliminating the open area in the design of these enclosures will help maintain negative air pressure necessary for containment of silica dust. Research conducted by the Partnership has shown that a well-enclosed drum housing and conveyor system can reduce workers’ dust exposure with as little as 900 actual cubic feet per minute (acfm) of air drawn from the primary conveyor and drum housing areas. The minimum flow rate of 900 acfm was determined to be effective in several tracer gas studies [NIOSH 2011c; 2012; 2013a].

Providing negative air pressure within an enclosure is a common ventilation technique for preventing a contaminant from escaping into surrounding areas. To contain silica dust, it is important to maintain negative air pressure in the drum housing of the milling machine. Operation of numerous water-spray nozzles within the drum housing can put the housing under positive air pressure. If exhaust ventilation is not used, dust-laden air can be forced out through gaps in the drum housing and contaminate the ambient surroundings, including the breathing zones of adjacent workers. The rotating drum and moving asphalt material may also generate air flows that can lead to dust escape from the drum housing. It is therefore important that the amount of open area through which leaks may occur from the drum housing be minimized to the extent compatible with the work process. The ventilation control should remove enough air to overcome any positive pressure and set a negative pressure differential between the drum housing and the surrounding air. Industrial Ventilation: A Manual of Recommended Practice for Design recommends a negative pressure differential of 0.04 +/- 0.02 inches of water as a good performance standard for containment of most industrial processes [ACGIH 2013b].

Typical ventilation controls designed to reduce dust exposures in a plant or on a piece of equipment consist of a hood, fan, ductwork, and dust collector [ACGIH 2013b]. If the ventilation control on a milling machine does not include a dust collector, the outlet from the system should discharge at high velocity in an upward orientation and be located near the top of the secondary conveyor or in another location away from workers. Milling machines without a dust collector should also be designed to allow the operator to temporarily turn the ventilation control off when milling into the wind. However, a feature should be in place to automatically turn the ventilation control back on when it has been off for longer than 60 minutes. Water-spray systems for cooling cutting teeth should remain on regardless of wind direction.

The ventilation control should be designed to have a minimum transport air velocity through the duct to prevent dust from settling and plugging the flow. The minimum duct design velocity recommended by American Conference of Governmental Industrial Hygienists (ACGIH) is 4,500 ft/min for heavy or moist dust [ACGIH 2013b].

Duct transport velocities alone may not be enough to prevent plugging. It is also important to design a gradual transition of air velocities between the duct and the take-off point of the dust control hood so that larger particles do not enter and clog the duct or damage the fan. The fan could move air from the drum housing or primary conveyor through a hood or settling box to gradually transition the air velocity from low to high before air enters the duct. The design intent of the ventilation control should be to at least control respirable size silica particles. It may also be prudent to design the ventilation control to capture inhalable size dust particles up to 100 μm in diameter. Particles less than 10 μm are capable of entering the gas exchange region of the lungs and triggering silicosis and cancer [Plog 2002].

Aerosol scientists have developed a spreadsheet that can be used to calculate settling velocity based on dust particle size and other factors [Baron and Willeke 2001]. Milling machine manufacturers should use the information about particle settling velocity to design a gradual transition of air velocities that prevent larger particles from entering the duct. A possible design would be to orient a hood or settling box so that air is pulled vertically from the drum housing or conveyor. Figure 2 shows a square settling box designed to settle out larger particles by gradually transitioning air velocities from low to high before dust enters the duct.

Even with a settling box or hood to provide a gradual transition of air velocities, the fan and ductwork should be designed to withstand a dusty airstream. The durability of the fan and duct work should be evaluated during the design and testing phase of the ventilation control. Any deficiencies in durability of the fan and duct work or clogging should be corrected before implementing the ventilation control across a fleet of milling machines.

Water Spray Application Guidelines for Asphalt Milling Machines

The Partnership conducted considerable research to develop best practice recommendations for water-spray dust suppression on asphalt milling machines. NIOSH recommends using best practice water-spray systems on asphalt milling machines that do not have ventilation controls. Water-spray systems can provide an effective and economical method to control dust in many types of industrial applications. Although the use of water sprays is a very simple technique, a number of factors should be evaluated to determine the most effective design for their use on asphalt pavement milling machines. Two effective dust control methods utilizing water sprays that are readily applicable to asphalt pavement milling operations are dust prevention and suppression techniques. Dust prevention is achieved by spraying water onto the pavement being milled in order to prevent dust from being liberated/generated and becoming airborne. The second method, dust suppression, involves knocking down airborne dust by spraying the dust cloud and causing the particles to collide, agglomerate, and fall from the air. A common and effective practice is to use a combination of both of these wet methods in the overall dust control plan. Since water is used on all asphalt pavement-milling machines to cool the cutter bits, it is logical to also use this water for respirable dust control.

The primary dust prevention technique is to wet road material (asphalt pavement) during milling, thus causing the material, fines, and dust particles to increase in weight. This in turn, decreases the ability for these dust particles to become airborne. As groups of particles become heavier, it becomes more difficult for the surrounding air to carry them off. The keys to effective wet spray dust control are (1) water pressure and water flow rate, (2) the proper application of moisture, (3) the careful design of nozzle location and orientation, (4) the control of droplet size, (5) the selection of the best spray pattern and spray nozzle type, and (6) the proper maintenance of nozzles and water spray application equipment [NIOSH 2010]. To the extent possible, the tanks, pumps, lines and nozzles in a dust suppression system should be made of non-corrosive or corrosion resistant materials. One last consideration is to have a properly designed liquid filtration system prior to the water application to minimize contaminants in the system and, ultimately, to prevent clogged water spray nozzles. NIOSH Best Practices for Dust Control in Metal/Nonmetal Mining provides more detailed information about spray nozzle selection and settings that have been effective in dust control for underground mining machines that share similar technology with cutter drums on milling machines [NIOSH 2010].

During the initial separation from the road bed, adequate wetting is extremely important to ensure that dust particles stay attached to the broken asphalt pavement material. Uniform wetting is also an important issue for an effective system. Dust reductions can be achieved by spraying the milled material with water while using the cutter drum to mechanically mix the asphalt pavement and water together to achieve uniform wetting [NIOSH 2011d]. The water sprays can cool the cutting bits on the milling drum and also provide dust suppression. Figure 3 illustrates water nozzles spraying the bits on a cutter drum. To conserve water, the water sprays should only be activated during milling. It is also recommended that manufacturers install water flow meters and pressure gauges on each machine to allow for visual determination that the water spray system is operating within the designed operating range.

Water Spray Application—Case Studies

In cooperation with NAPA, milling contractors, and equipment manufacturers, NIOSH evaluated the effectiveness of changes in water spray applications on multiple pavement milling job sites. During these surveys, respirable dust levels were measured at multiple locations around the milling machine to monitor dust liberation from the cutter housing and lower conveyor transfer locations. Descriptions of the sampling procedures used during these surveys and specific test conditions at each site are provided in technical reports referenced with each case study. Not all water spray modifications were successful, but multiple surveys did provide examples of measurable reductions in dust liberation. Several case studies are summarized below to illustrate the modifications and changes in water spray application and their measured benefits.

Case Study A

On this milling machine, baseline dust levels were determined with the water spray system operated at levels routinely used during milling. The system was equipped with 18 flat-fan sprays (i.e. nozzles) located behind the cutter drum, five flat-fan sprays at the front of the cutter drum, and several sprays at the transition from the primary conveyor. The water pump on the milling machine could be adjusted and had a rated output up to 15 gallons per minute (gpm) at 200 pounds per square inch (psi). However, the water spray system levels routinely used during milling were 6 gpm at 35 psi.

Adjustments were made to the pump to increase the water pressure from 35 psi to 70 psi with a corresponding increase in water flow from 6 gpm to 12 gpm. Figure 4 shows a typical water flow meter and pressure gauge that were installed and used to quantify water application changes during testing. Measurements from seven area dust sampling locations around the machine resulted in a 50% reduction (from a geometric mean of 1 mg/m³ to 0.5 mg/m³) in respirable dust by simply adjusting the water pump from the operator’s deck from 35 to 70 psi, without any change or addition to the existing spray nozzles [NIOSH 2007a]. Personal breathing zone air sampling results for respirable crystalline silica ranged from less than the limit of detection to 0.170 mg/m³ for the trial time sampled [NIOSH 2007a].

Case Study B

Similar to Case Study A, the water flow to this milling machine could be adjusted by the operator by changing the output from the water pump. During this survey, increases in water flow from 12.5 gpm to 18.8 gpm resulted in respirable dust reductions of approximately 41% (from a geometric mean of 0.328 mg/m³ to 0.193 mg/m³) at 10 key area sampling locations around the machine [NIOSH 2009b]. Once again, these dust reductions were achieved without making changes to the existing water spray system other than increasing the water pump output.

Case Study C

During this evaluation, the baseline water spray system consisted of a total of 16 water spray nozzles located at the front and rear of the cutter housing and at the discharge to the primary conveyor. Total water flow for these nozzles was 22.4 gpm at 20 psi. For the modified spray system, a total of 14 nozzles were used, which supplied 21.4 gpm at 20 psi. In this case study, water quantity was not increased, but changes to the distribution of the water, such as spray nozzle location and orientation, improved dust control. For example, nozzles were relocated in the front of the cutter housing to discharge water in the opposite direction of material flow, the upper front-housing sprays were eliminated, and sprays were added to the primary conveyor transition. Respirable dust levels measured for the modified spray system at six key area sampling locations on the machine resulted in an average dust reduction of approximately 43% (from a geometric mean of 0.72 mg/m³ to 0.41 mg/m³) when compared to baseline dust levels [NIOSH 2011d].

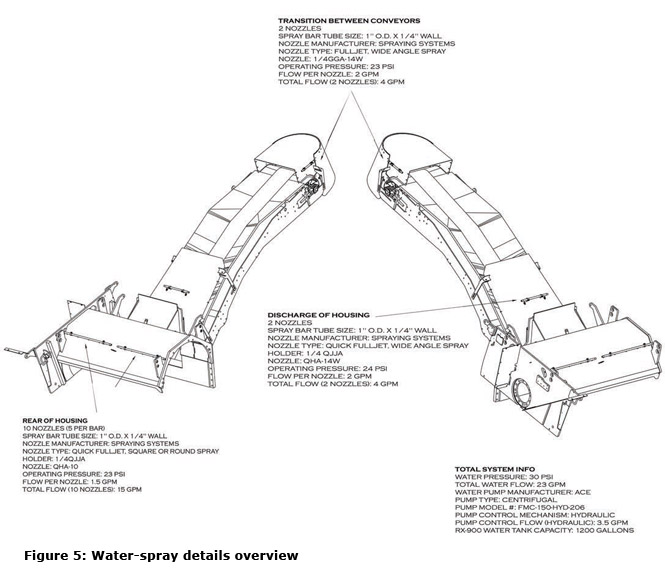
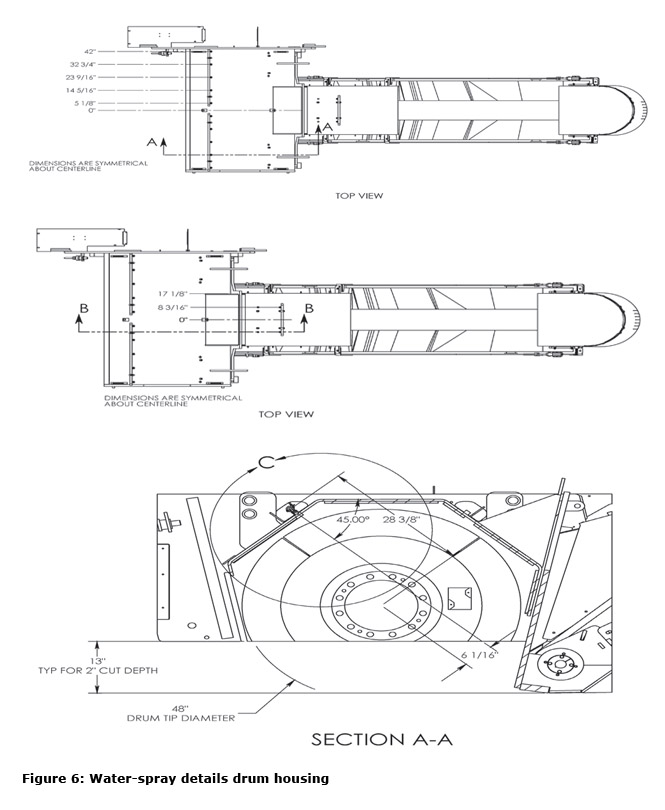
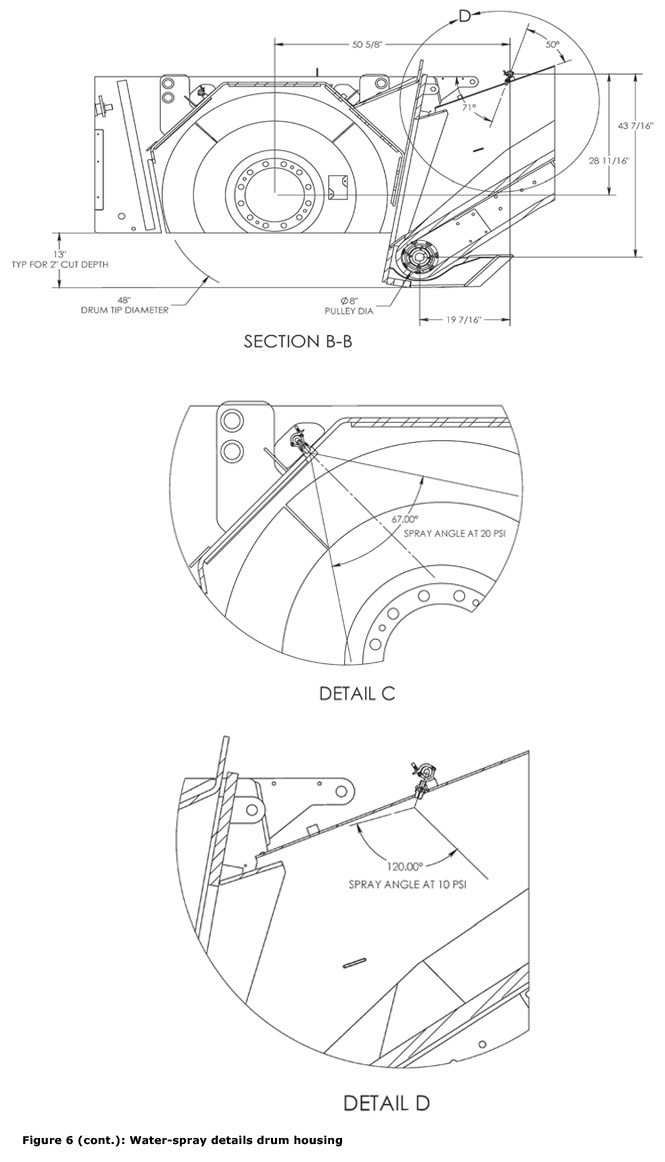
The Partnership determined that Case Study C was the most effective dust control configuration evaluated on a new asphalt milling machine and engineering drawings are provided in Figures 5-7. However, this recommendation should not limit manufacturers from implementing future improvements in water-spray dust control as new technologies, configurations, or inventions are evaluated.

 

 

 

 

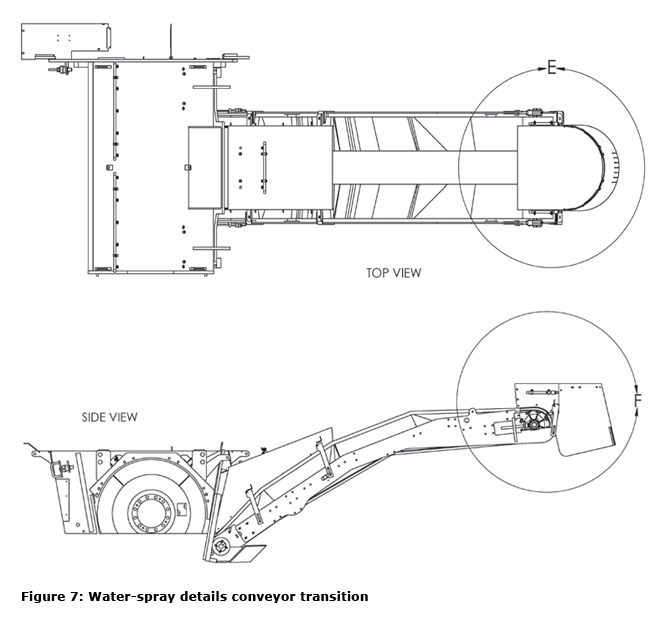
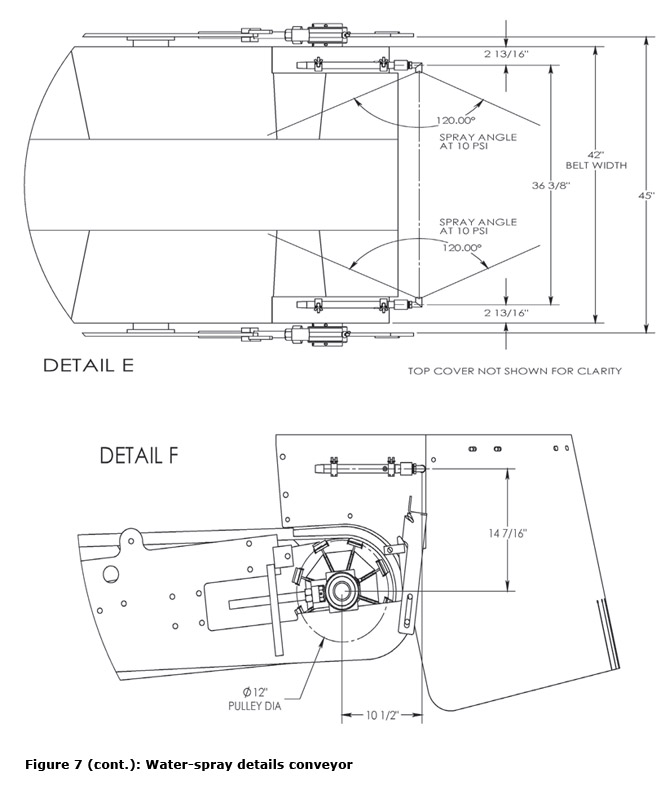
Wet Drum Studies

In addition to multiple evaluations of water spray configurations, NIOSH and the Partnership also evaluated the utilization of wet drum technology. With the wet drum, water is supplied to the inside of the cutting drum and uses gravity to release water through nozzles in the drum housing in an effort to prevent the release of dust in the cutting area. The dust levels obtained with the wet drum were compared to dust levels generated by the baseline water spray system, which consisted of sprays located along the back side of the cutting drum and sprays at the primary and secondary conveyor transfer locations. The wet drum technology was evaluated at two different milling sites. At the first test site, utilization of the wet drum resulted in a 32% reduction at the lower sampling locations and a dust reduction of 59% at the operator location [NIOSH 2011c]. At the second test site, the wet drum resulted in average dust reductions of 37% at the lower sampling locations and 27% at the operator location [NIOSH 2013d]. However, due to wide performance variability, the reductions at the second site were not statistically significant. Personal breathing zone air sampling results for respirable crystalline silica ranged from 0.028 mg/m³ to 0.085 mg/m³ at the second wet drum test site [NIOSH 2013d].

One problem observed with the operation of the wet drum technology was inconsistent water distribution from the drum. On level roadways, water was discharged from the drum evenly across the entire milled strip. However, if the roadway was not level across its width, water would discharge from the low side of the cutter drum but the roadway on the high side of the drum would be dry. Baffles added inside the drum to ensure uniform water distribution to all sections of the drum might potentially improve the performance of the wet drum technology.

NIOSH Recommended Best Practice Test Guidance for Dust Controls on Milling Machines

• NIOSH recommend that each milling machine manufacturer design and install ventilation controls with a minimum indoor capture efficiency of at least 90% (as determined by the tracer gas method described in Appendix A) on all new half-lane and larger cold-milling machines. Each milling machine manufacturer should conduct the tracer gas testing of ventilation controls for a representative design of a half-lane and full-lane new milling machine. Manufacturers should consider re-testing future milling machine designs if appreciable changes are made that could negatively impact the effectiveness of the ventilation control.
• Manufacturers should install an air-flow indicating device on each milling machine so that the ventilation control flow rate can be monitored. The device should allow for visual determination that the ventilation control is operating within the designed operating range. Each manufacturer should attach a plate to the milling machine showing a simple diagram of the ventilation control and a list of field-maintenance procedures.
• NIOSH recommends that each manufacturer should use the procedures in Appendix B to conduct field testing of a representative design of a half-lane and full-lane new milling machine equipped with ventilation controls. The purpose of the field testing is to verify that the ventilation controls continue to protect workers during asphalt pavement milling.
• The ventilation and water-spray dust controls described in this document represent the current knowledge of best practices developed by the Partnership for controlling dust during asphalt pavement milling. This document should not limit manufacturers from implementing future improvements in dust control as new technologies or inventions become available. Manufacturers can use the procedures in Appendix B to evaluate current and future dust controls. Appendix D provides instructions on how to use the spreadsheet that accompanies the statistical procedures explained in Appendix B.
• Milling machine contractors should implement a water-spray and ventilation control system daily checklist to verify that the dust controls are being operated according to the manufacturer instructions. An example daily checklist is provided in Appendix E.

Recommendations for Operation and Maintenance of Dust Control Systems

Cold-milling machine manufacturers should provide an operator’s manual that contains a maintenance schedule for the water-spray or ventilation controls. Each operator’s manual should also include detailed sketches, performance criteria, and troubleshooting instructions for equipment owners to use in their periodic inspection of these controls. Owners of cold-milling machines equipped with these dust control systems are advised to inspect and maintain the systems according to the manufacturer’s recommendations and to record the dates of periodic inspections in the operator’s manual.

Training

Equipment manufacturers should provide training manuals to equipment owners in the operation, maintenance, and repair of their dust control systems for cold-milling machines. Equipment mechanics trained in the maintenance and repair of cold-milling machines may require additional training to be aware of and perform these services on the dust control systems. Milling machine operators should also be trained on these controls and be provided with the desired operating specifications (water quantity, water pressure, air velocity) that must be maintained to be effective. Also, milling machine operators should be trained to temporarily disable the ventilation control system when milling directly into the wind.

Additionally, NAPA has published a Best Practice Bulletin 1/12, Operational Guidance for Water Systems During Milling Operations, which is reprinted in Appendix F of this document with permission from NAPA. The NAPA Best Practices Bulletin 1/12 is free of charge and provides additional information about maintaining water-spray systems during milling operations.

Silica and Health Effects

Silica (SiO₂), an oxide of silicon, occurs in nature as a mineral in quartz, chalcedony, chert, flint, opal, diatomaceous earth, and sandstone [USGS 1914]. “Crystalline” refers to the orientation of the SiO₂ molecules in a fixed pattern as opposed to a nonperiodic, random molecular arrangement defined as amorphous [NIOSH 1974]. The three most common forms of crystalline silica encountered in construction and mining are quartz, tridymite, and cristobalite. NIOSH defines respirable crystalline silica as

“that portion of airborne crystalline silica that is capable of entering the gas-exchange regions of the lungs if inhaled; by convention, a particle-size-selective fraction of the total airborne dust; includes particles with aerodynamic diameters less than approximately 10 μm and has a 50% deposition efficiency for particles with an aerodynamic diameter of approximately 4 μm” [NIOSH 2002].

NIOSH estimates that at least 1.7 million American workers are exposed to respirable crystalline silica and that many of those workers’ exposures exceed current occupational exposure limits [NIOSH 2002]. Inhalation of respirable crystalline silica can cause silicosis, a debilitating and potentially fatal lung disease. Silica exposure has also been associated with lung cancer, chronic obstructive pulmonary disease, renal disease, and other adverse health outcomes [NIOSH 2002]. During the period from 1990 through 1999, at least one-third of decedents with silicosis had worked in construction or mining [NIOSH 2007b].

Occupational Exposure Limits

In the United States, occupational exposure limits (OELs) have been established by federal agencies, professional organizations, state and local governments, and other entities. The U.S. Department of Labor OSHA permissible exposure limits (PELs) [29 CFR 1910.1000 (2003)] are OELs that are legally enforceable in covered workplaces under the Occupational Safety and Health Act. NIOSH issues RELs that are based on a critical review of the scientific and technical information available on the prevalence of health effects, the existence of safety and health risks, and the adequacy of methods to identify and control hazards [NIOSH 1992]. Other OELs that are commonly used and cited in the United States include the Threshold Limit Values (TLVs) recommended by ACGIH [ACGIH 2013a]. ACGIH TLVs are considered voluntary guidelines for use by industrial hygienists and others trained in this discipline “to assist in the control of health hazards.” Workplace environmental exposure levels (WEELs) are recommended OELs developed by the American Industrial Hygiene Association (AIHA). WEELs have been established for some chemicals “when no other legal or authoritative limits exist” [AIHA 2007].

OSHA requires an employer to furnish employees a place of employment that is free from recognized hazards that are causing or are likely to cause death or serious physical harm (Occupational Safety and Health Act of 1970, Public Law 91–596, sec. 5(a)(1)). Thus, employers are required to comply with OSHA PELs. NIOSH investigators also encourage employers to consider other OELs in making risk assessment and risk management decisions to best protect the health of their employees. NIOSH investigators encourage the use of the traditional hierarchy-of-controls approach to eliminating or minimizing identified workplace hazards. This approach includes, in preferential order, the use of (1) substitution or elimination of the hazardous agent, (2) engineering controls (e.g., local exhaust ventilation, process enclosure) (3) administrative controls (e.g., limiting time of exposure, employee training, work practice changes, medical surveillance), and (4) personal protective equipment (e.g., respiratory protection, gloves, eye protection, hearing protection).

Crystalline Silica Exposure Limits

The NIOSH REL for respirable crystalline silica is 0.05 mg/m³ as a time-weighted average (TWA) determined during a full-shift personal breathing zone sample. This REL is applicable for most workers who work up to a 10-hr workday during a 40-hr workweek to reduce the risk of developing silicosis, lung cancer, and other adverse health effects [NIOSH 2002].

The current OSHA PEL for respirable dust containing crystalline silica for the construction industry is measured by impinger sampling. In the construction industry, the PELs for cristobalite and quartz are the same.

Since the PELs were adopted, the impinger sampling method has been rendered obsolete by respirable dust gravimetric sampling [OSHA 1996]. OSHA currently instructs its compliance officers to apply a conversion factor when converting between gravimetric sampling and the particle count standard when characterizing construction operation exposures [OSHA 2008].

On September 12, 2013, OSHA published a Notice of Proposed Rulemaking (NPRM) for occupational exposure to respirable crystalline silica. The NPRM was published in the Federal Register and proposes a PEL of 0.05 mg/m³ for respirable crystalline silica as an 8-hr TWA exposure [78 Fed. Reg. 56274 (2013)].

The ACGIH TLV for quartz and cristobalite (respirable fraction) is 0.025 mg/m³ as an 8-hr TWA exposure [ACGIH 2013a]. The documentation to the TLV states that “it is the concern about fibrosis (silicosis) and the precedent inflammatory process resulting from silica exposures, and the association of inflammation and fibrosis with lung cancer that leads to this recommendation [ACGIH 2010].”

References

78 Fed. Reg. 56274 [2013]. Occupational exposure to respirable crystalline silica, a proposed rule.

ACGIH [2010]. 2010 Documentation to the TLV silica, crystalline – α-quartz and cristobalite. Cincinnati, OH: American Conference of Governmental Industrial Hygienists.

ACGIH [2013a]. 2013 Threshold Limit Values (TLVs) and Biological Exposure Indices (BEIs). Cincinnati, OH: American Conference of Governmental Industrial Hygienists.

ACGIH [2013b]. Industrial ventilation: a manual of recommended practice for design. 28^th edition. Cincinnati, OH: American Conference of Governmental Industrial Hygienists.

AIHA [2007]. 2007 Emergency response planning guidelines (ERPG) & workplace environmental exposure levels (WEEL) handbook. Fairfax, VA: American Industrial Hygiene Association.

Akbar-Khanzadeh F, Brillhart RL [2002]. Respirable crystalline silica dust exposure during concrete finishing (grinding) using hand-held grinders in the construction industry. Ann Occup Hyg 46(3):341–346.

Baron PA, Willeke K [2001]. Aerosol measurement principles, techniques, and applications. 2^nd edition. Hoboken, NJ: John Wiley and Sons, Inc.

CFR. Code of Federal Regulations. Washington, DC: U.S. Government Printing Office, Office of the Federal Register.

Glindmeyer HW, Hammad YY [1988]. Contributing factors to sandblasters’ silicosis: inadequate respiratory protection equipment and standards. J Occup Med 30(12):917–921.

Linch KD [2002]. Respirable concrete dust—silicosis hazard in the construction industry. Appl Occup Environ Hyg 17(3):209–221.

NIOSH [1974]. Criteria for a recommended standard—occupational exposure to crystalline silica. Cincinnati, OH: U.S. Department of Health, Education, and Welfare, Center for Disease Control, National Institute for Occupational Safety and Health, HEW Publication No. (NIOSH) 75-120.

NIOSH [1992]. Recommendations for occupational safety and health: compendium of policy documents and statements. Cincinnati, OH: U.S. Department of Health and Human Services, Centers for Disease Control, National Institute for Occupational Safety and Health, DHHS (NIOSH) Publication No. 92-100.

NIOSH [1997]. Engineering control guidelines for hot mix asphalt pavers. Cincinnati, OH: Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, DHHS (NIOSH) Publication No. 97-105.

NIOSH [1998]. Particulates not otherwise regulated, respirable. Cincinnati, OH: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, DHHS (NIOSH) Publication No. 81-123.

NIOSH [2000]. Respirable crystalline silica exposures during tuck pointing. Cincinnati, OH: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, DHHS (NIOSH) Publication No. 2000-113.

NIOSH [2002]. NIOSH hazard review: health effects of occupational exposure to respirable crystalline silica. Cincinnati, OH: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, DHHS (NIOSH) Publication No. 2002-129.

NIOSH [2003]. Silica, crystalline, by XRD (filter redeposition). Cincinnati, OH: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, DHHS (NIOSH) Publication No. 2003-154.

NIOSH [2004]. Results of a pilot study of dust control technology for asphalt milling, at Payne & Dolan, Inc., U.S. route 12 project, Wisconsin. By Echt A, Shulman S, Colinet J, Goodman G. Cincinnati, OH: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, EPHB Report No. 282-11b [http://www.cdc.gov/niosh/surveyreports/pdfs/282-11b.pdf].

NIOSH [2007a]. In-depth survey of dust control technology for asphalt milling, at Northeast Asphalt, Inc., state routes 22 and 64 projects, Wisconsin. By Echt A, Garcia A, Shulman S, Colinet J, Cecala A, Carlo RV, Zimmer J. Cincinnati, OH: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, EPHB Report No. 282-12a [http://www.cdc.gov/niosh/surveyreports/pdfs/282-12a.pdf].

NIOSH [2007b]. Silicosis: most frequently recorded industries on death certificate, U.S. residents age 15 and over, selected states and years, 1990–1999, Table 3-6. In: NIOSH work-related lung disease surveillance report 2007. Cincinnati, OH: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, DHHS (NIOSH) Publication No. 2008–143a.

NIOSH [2009a]. In-depth field evaluation: dust-control technology for asphalt pavement milling, at New York State Thruway (Interstate Highway 90) resurfacing project, Hamburg, New York, September 25 and 26, 2006. By Blade LM, Shulman SA, Garcia A, Marlow DA. Cincinnati, OH: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, EPHB Report No. 282-16a [http://www.cdc.gov/niosh/surveyreports/pdfs/282-16a.pdf].

NIOSH [2009b]. In-depth field evaluation: dust-control technology for asphalt pavement milling, at South Dakota Highway 79 resurfacing project, Buffalo Gap, South Dakota, August 15 through 17, 2006. By Blade LM, Garcia A, Shulman SA, Colinet J, Chekan G. Cincinnati, OH: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, EPHB Report No. 282-14a [http://www.cdc.gov/niosh/surveyreports/pdfs/282-14a.pdf].

NIOSH [2009c]. In-depth field evaluation: dust-control technology for asphalt pavement milling, at U.S Highway 2 resurfacing project, Wilton, Minnesota, June 20 through 22, 2006. By Blade LM, Shulman SA, Colinet J, Chekan G, Garcia A. Cincinnati, OH: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, EPHB Report No. 282-15a [http://www.cdc.gov/niosh/surveyreports/pdfs/282-15a.pdf].

NIOSH [2010]. Information circular 9521: best practices for dust control in metal/nonmetal mining. By Colinet JF, Cecala AB, Chekan GJ, Organiscak JA, Wolfe AL. Cincinnati, OH: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, DHHS (NIOSH) Publication No. 2010-132.

NIOSH [2011a]. A laboratory evaluation of a prototype local exhaust ventilation system on a Terex cold milling machine at Terex Roadbuilding, Oklahoma City, Oklahoma. By Hammond DR, Mead KR, Trifonoff N, Shulman SA. Cincinnati, OH: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, EPHB Report No. 282-20a [http://www.cdc.gov/niosh/surveyreports/pdfs/282-20a.pdf].

NIOSH [2011b]. A laboratory evaluation of capture efficiencies of the vacuum cutting system on a Wirtgen W 250 cold milling machine at Payne & Dolan Inc., Racine, Wisconsin. By Hammond DR, Trifonoff N, Shulman SA. Cincinnati, OH: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, EPHB Report No. 282-19a [http://www.cdc.gov/niosh/surveyreports/pdfs/282-19a.pdf].

NIOSH [2011c]. Dust-control technology for asphalt-pavement milling controlled-site testing at State Highway 47, Bonduel, Wisconsin. By Hammond DR, Blade LM, Shulman SA, Zimmer J, Cecala AB, Joy GJ, Lo LM, Chekan GJ. Cincinnati, OH: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, EPHB Report No. 282-18a [http://www.cdc.gov/niosh/surveyreports/pdfs/282-18a.pdf].

NIOSH [2011d]. In-depth survey report: dust-control technology for asphalt pavement milling. By Blade LM, Shulman SA, Cecala A, Chekan G, Zimmer J, Garcia A, Lo LM, Calahan J. Cincinnati, OH: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, EPHB Report No. 282-17a [http://www.cdc.gov/niosh/surveyreports/pdfs/282-17a.pdf].

NIOSH [2012]. A laboratory evaluation of a local exhaust ventilation system on a Caterpillar cold milling machine at Caterpillar, Minnesota. By Hammond DR, Garcia A, Henn S, Shulman SA. Cincinnati, OH: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, EPHB Report No. 282-22a [http://www.cdc.gov/niosh/surveyreports/pdfs/282-22a.pdf].

NIOSH [2013a]. A laboratory evaluation of a local exhaust ventilation system on a Roadtec cold milling machine at Roadtec, Chattanooga, Tennessee. By Hammond DR, Garcia A, Shulman SA.Cincinnati, OH: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, EPHB Report No. 282-21a [http://www.cdc.gov/niosh/surveyreports/pdfs/282-21a.pdf].

NIOSH [2013b]. Control technology for crystalline silica exposure during pavement milling using a Roadtec milling machine equipped with a local exhaust ventilation system. By Hammond DR, Shulman SA Cincinnati, OH: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, EPHB Report No. 282-25a [http://www.cdc.gov/niosh/surveyreports/pdfs/282-25a.pdf].

NIOSH [2013c]. Control technology for crystalline silica exposure during pavement milling using a Wirtgen milling machine equipped with a vacuum cutting system. By Hammond DR, Shulman SA. Cincinnati, OH: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, EPHB Report No. 282-23a [http://www.cdc.gov/niosh/surveyreports/pdfs/282-23a.pdf].

NIOSH [2013d]. Evaluation of a Volvo milling machine equipped with a wet drum designed to reduce respirable crystalline silica exposure during pavement milling. By Hammond DR, Kovein R, Shulman SA. Cincinnati, OH: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, EPHB Report No. 282-24a [http://www.cdc.gov/niosh/surveyreports/pdfs/282-24a.pdf].

OSHA [1996]. Appendix F: permissible exposure limits for construction and maritime. In: Memorandum of May 2, 1996, from Joseph A. Dear, Occupational Safety and Health Administration, to regional administrators.

OSHA [2008]. Appendix E: conversion factor for silica PELs in construction and maritime. In: National emphasis program—crystalline silica. Washington, DC: Occupational Safety and Health Administration, CPL 03-00-007 [http://www.osha.gov/pls/oshaweb/owadisp.show_document?p_table=DIRECTIVES&p_id=3790#e].

Plog BA, Quinlan PJ [2002]. Fundamentals of industrial hygiene. 5^th edition. Itasca, IL: National Safety Council.

Public Works [1995]. Pavement recycling. Public Works 126.

Rappaport SM, Goldberg M, Susi P, Herrick RF [2003]. Excessive exposure to silica in the U.S. construction industry. Ann Occup Hyg 47(2):111–122.

Thorpe A, Ritchie AS, Gibson MJ, Brown RC [1999]. Measurements of the effectiveness of dust control on cut-off saws used in the construction industry. Ann Occup Hyg 43(7):443–456.

U.S. Census Bureau [2007]. Industry statistics sampler. NAICS 237310. Highway, street, and bridge construction. Washington, DC: U.S. Department of Commerce.

USGS [1914]. Useful minerals of the United States. Washington, DC: U.S. Department of the Interior, United States Geological Survey, Bulletin 585.

Valiante DJ, Schill DP, Rosenman KD, Socie E [2004]. Highway repair: a new silicosis threat. Am J Public Health 94(5):876–880.

Appendix A: Laboratory tracer gas test procedures to evaluate ventilation controls on asphalt pavement milling machines

These tracer gas laboratory test procedures were adopted from the document titled Engineering Control Guidelines for Hot Mix Asphalt Pavers [NIOSH 1997] and modified for asphalt pavement milling machines. These test procedures are the result of a collaborative effort by labor, industry, and government to reduce respirable crystalline silica exposure during asphalt pavement milling in highway construction.

Purpose

This test procedure is a first step in evaluating the capture efficiency of milling machine ventilation controls and is conducted in an indoor stationary environment before field testing. The goal of the test is to optimize the ventilation controls using tracer gas as a surrogate for respirable crystalline silica. This test can only approximate actual milling conditions, and actual milling conditions may give different results. The test will not evaluate filtration efficiency of ventilation controls if so equipped with a dust collection system.

Tracer gas studies have been completed for four milling machine manufacturers who are Partnership members. NIOSH technical reports from those studies can also be used to assist manufacturers of new asphalt milling equipment models in conducting tracer gas testing of their asphalt pavement milling machines [NIOSH 2011a, NIOSH 2011b; NIOSH 2012; NIOSH 2013].

Equipment/Facilities/Materials

• Two properly calibrated tracer gas monitors
• Asphalt pavement milling machine fitted with ventilation controls designed to prevent exposure to respirable crystalline silica
• Building with large opening (overhead door) to the outdoors
• Materials to construct a barrier, such as cardboard, plastic sheeting or tarpaulins, lumber of varying length, and duct tape
• Smoke generator
• PVC pipe: 5-centimeter (2-inch), schedule 40, 3 meters (10 feet) long, capped on one end, holes 6.4 millimeters (1/4 inch) in diameter drilled in a line every 15 centimeters (6 inches) on center (smoke distribution pipe)
• Tracer gas cylinder with dual stage pressure regulator fitted with an on/off valve after the second stage
• Zero air or nitrogen cylinder
• A tracer gas detector capable of measuring the selected tracer gas
• Polytetrafluoroethylene (PTFE) tubing: 3.2-millimeter (1/8-inch) outside diameter, 4 meters (13 feet) long
• Copper pipe: 12.7-millimeter (1/2-inch) inside diameter, the same length as the drum width, holes 0.79 millimeters (1/32 inch) in diameter drilled in a straight line 30 centimeters (12 inches) on center (tracer gas distribution pipe)
• Polyethylene (PE) tubing: 6.4-millimeter (1/4-inch) outside diameter, 30 meters (100 feet) long
• Two mass flow controllers with shut-off valves and a range appropriate for the selected tracer gas and zero air
• Bubble meter: 0.5-liter graduated cylinder, soap solution, and stop watch to measure gas flow rates; or a calibrated electronic flow calibrator
• Stainless steel tubing: 6.4-millimeter (1/4-inch) outside diameter, 30 centimeters (12 inches) long (sampling probe), sealed at one end, holes 1.6 millimeters (1/16 inch) in diameter drilled in a straight line 2.54 centimeters (1 inch) on center starting 2.54 centimeters (1 inch) from the sealed end (The number of holes will depend upon the diameter of the ventilation exhaust duct: a 20-centimeter [8-inch] exhaust duct requires the use of a sampling probe with seven holes 1.6 millimeters [1/16 inch] in diameter.)
• Manometer and pitot tube

Safety

The following safety precautions must be taken for each test:

• Use caution when handling smoke-generating equipment: it can be HOT!
• Make sure that the smoke generator does not set off fire sprinklers or create a false alarm.
• Avoid direct inhalation of smoke from the smoke generator. The smoke may act as an irritant in the upper respiratory tract.
• Transport, handle, and store all compressed gas cylinders according to the safety recommendations of the Compressed Gas Association (CGA) [CGA 2008].
• During testing, locate the compressed gas cylinder outdoors or in a well-ventilated area. The temperature should not exceed 125°F in the storage location.
• Avoid breathing the gas if a gas cylinder regulator malfunctions or some other major accidental release occurs. A major release of gas could displace the ambient air and reduce the oxygen level in the environment. Clear the area, and let the tank pressure reach equilibrium with the ambient environment. Wait until the concentration is below any applicable OEL before re-entering the area. Refer to the material safety data sheet (MSDS) or applicable OSHA PELs, NIOSH RELs or ACGIH TVLs for the safe level of the gas.

Procedures

General

These procedures are for testing the ventilation controls adapted to half-lane and larger milling machines for the control of respirable crystalline silica during asphalt pavement milling. These test procedures do not cover engine exhaust. The purpose of this testing is to optimize design parameters by evaluating different ventilation control flow rates.

Prepare the machine for testing as outlined below:

1. Position the milling machine in a bay area of a plant or garage with the outlet ducts placed through an opening leading to the outdoors.
2. Seal the building openings using cardboard, plastic, or other materials as shown in Figure A. This will help prevent tracer gas from recirculating back into the building.
3. Use wood, cardboard, or other materials to block off open areas between the cutting drum housing and the floor. These areas would normally be blocked by the ground during pavement milling due to the drum being below the surface of the road.
4. The indoor area surrounding the milling machine should be sufficiently large such that any tracer gas that escapes the drum housing is allowed to dissipate within the room without being drawn back into the drum housing area.
5. Position the cutting drum and conveyor as close as possible to the configuration used when milling. For example, the secondary conveyor should be at approximately the same height and angle as used in a typical pavement milling job.
6. Measure the duct velocity of the ventilation controls before and after tracer gas tests at each air flow rate. Information on how to measure duct velocity can be found in the “Testing and Measurement of Ventilation Systems” section in Industrial Ventilation: A Manual of Recommended Practice for Operation and Maintenance [ACGIH 2007].
7. During the performance evaluations, turn on the conveyors and set the engine to the speed typical for normal milling operations. The cutting drum should be rotating during the smoke and tracer gas tests to better replicate airflow patterns in the drum housing.

Smoke Test

The smoke test is designed to ensure that the barrier at the doorway is adequate for the quantitative tracer gas test and to visualize airflow patterns around the milling machine and conveyor areas. If smoke escapes from the drum housing or primary conveyor area, the air flow rate of the ventilation controls should be increased. If smoke leaks back into the building, seal any leaks in the barrier to the outdoors.

The sequence of a typical smoke test is outlined below:

1. Verify that the smoke generated by the test will not set off a fire alarm or fire-suppression system.
2. Place the 2-inch-diameter smoke distribution pipe directly beneath the cutter drum within 2 inches of the drum and secure in a horizontal position so that the holes are oriented upward on center with the cutter drum.
3. Use duct tape to block any holes in the smoke distribution pipe that extend beyond the width of the drum so that smoke is only released under the drum.
4. Connect the smoke generator to the smoke distribution pipe.
5. Clear the cutter drum area of any extraneous materials.
6. With the ventilation control on and the drum and conveyor running, release smoke in the drum area and look for leaks around the machine and through the barrier blocking smoke from coming in from the outdoors. Inspect the ventilation controls for unintended leaks at all fittings.
7. With the drum and conveyor running for a short time, deactivate the ventilation controls. This step is for simulating a no-control condition for comparison purposes.
8. Deactivate the smoke generator and wait for smoke levels to subside. If necessary to clear the room quickly, turn on additional exhaust ventilation.
9. Disassemble the test equipment (CAUTION!! The smoke generator may be HOT).
10. Repeat this test if substantial changes are made to the setup.

Tracer Gas Test

The tracer gas test is designed to calculate the volumetric air flow rate of the milling machine ventilation controls and to evaluate the system’s effectiveness in capturing a surrogate contaminant under controlled indoor conditions. A tracer gas appropriate for ventilation testing should be used as the surrogate contaminant. A pitot tube traverse using procedures outlined in the Industrial Ventilation Manual should also be conducted to measure the ventilation system’s air flow rate [ACGIH 2007]. The air flow rate determined from the pitot tube measurements should be compared with the tracer gas air flow rate calculations.

Ensure that the tracer gas detector has been calibrated according to manufacturer recommendations. Before testing begins, calibrate the mass-flow controllers with a bubble meter and a timer or with a calibrated electronic flow calibrator. Allow the tracer gas to flow through the pressure regulator to the mass-flow controllers to regulate the flow rate. Direct the flow through the wet bubble meter or calibrated electronic flow calibrator to determine the actual tracer gas flow rate [NIOSH 1973].

The 100% Capture Test

The purpose of conducting the 100% capture test is to provide another measure of the ventilation control air flow rate and to determine the concentration at which all of the tracer gas is captured for use in the capture efficiency calculation. The 100% capture test is completed by releasing a known rate of tracer gas into the ventilation control and sampling the diluted concentration of the tracer gas at a well-mixed location downstream in the ventilation exhaust duct. The accuracy of the mass flow controller calibration is pivotal to ensuring an accurate test. Releasing the tracer gas inside the intake to the ventilation controls will give the best chance for complete capture and mixing.

The sequence of the 100% capture test is outlined below:

1. Connect the supply tank of tracer gas to the release point using a pressure regulator, a mass-flow controller, and as much 6.4-millimeter (1/4-inch) tubing as needed to reach the tracer gas distribution pipe and the 100% tracer gas dosing (C100) locations.
2. Find a downstream sampling location in the duct where the tracer gas has been thoroughly mixed. If the sample is taken downstream of the fan, it should be sufficiently mixed. Long duct runs, sections of flexible duct, and duct fittings will also enhance mixing. If the gases are not thoroughly mixed, an extension on the exhaust duct may be needed.
3. If the air is thoroughly mixed, place a sampling hole 6.4 millimeters (1/4 inch) in diameter in the duct at least three duct diameters before the duct outlet. Insert the sampling probe through the sampling hole and position the holes in the sampling probe inside the duct and perpendicular to the direction of air flow. Secure the sample probe using tape. Sample tubing should connect the sampling probe to the detector and should be airtight to ensure that the sample is pulled from within the duct and not from the surrounding area.
4. Take at least five background measurements before starting the flow of tracer gas. Turn on the tracer gas and take at least five measurements during a 3-minute period and use the average of these concentration measurements to calculate the ventilation control air flow rate with Equation A-1. Before calculating the ventilation control flow rate (Q_(exh)), subtract background readings between sequential tests from the detector response. where Q(exh) is the flow rate of air exhausted through the ventilation system (liters/minute or cubic feet/minute) (to convert from liters/minute to cubic feet/minute, divide liters/minute by 28.3), Q(TG) is the flow rate of tracer gas (liters/minute or cubic feet/minute) introduced into the system, and C(100) is the average concentration of tracer gas (parts per million) detected in the duct during the five 100% tracer gas capture tests.
5. If there is more than one ventilation duct, repeat the above procedure for each duct.
6. Following each tracer gas release, flush the tracer gas delivery tubing system with zero air (or nitrogen) for 1 minute.
7. Allow sufficient time between tests for the background readings to decay to less than 1% of the 100% tracer gas capture concentration.

Quantitative Capture Efficiency Test

The quantitative capture efficiency test is conducted to determine the capture efficiency of the ventilation control and uses the results of the 100% capture test.

The sequence of a quantitative capture efficiency test is outlined below:

1. Leave the sample probe, sample tubing, and tracer gas detector in the same location and orientation as the 100% capture test.
2. Leave the supply tank, pressure regulator setting, and mass flow controller setting in the same position as the 100% capture test.
3. The release location of the tracer gas supply tubing should be removed from the 100% location and connected to the 12.7-millimeter (½-inch) copper tracer gas distribution pipe.
4. Position the tracer gas distribution pipe under the cutter drum and orient the holes of the distribution pipe up toward the center axle of the cutter drum.
5. Start the milling machine engine and set the engine at the speed (rpm) typical for normal milling operations. Start the ventilation control and begin monitoring for tracer gas to determine background levels.
6. To determine background concentration, take at least five measurements during a 3-minute period.
7. Release the tracer gas at the same mass flow controller setting used in the 100% capture test. The tracer gas distribution pipe is designed to release the tracer gas evenly throughout the width of the cutter drum area.
8. Wait 30 seconds for the tracer gas concentration to reach steady state then take at least five measurements during a 3-minute period and calculate an average concentration. Subtract background concentration, and calculate the capture efficiency (η) using Equation A-2.
9. Discontinue the tracer gas flow and flush the tracer gas distribution system with zero air (or nitrogen) for 1 minute.
10. Allow sufficient time between tests for the background readings to decay to less than 1% of the 100% tracer gas capture concentration.
11. Perform a total of five pairs of the 100% capture tests and capture efficiency tests and determine the overall capture efficiency of the ventilation control from the average of all five trials.

Analysis of Tracer Gas Data

The tracer gas data should be analyzed to determine if the average capture efficiency is sufficiently large to conclude that the true mean capture efficiency exceeds 90% with 95% confidence. This approach treats the efficiency values as a normally distributed random sample. The lower confidence limit for the true efficiency is obtained by using the t distribution [Agresti and Franklin 2009].

To accomplish this, compute the lower 95% confidence limit for the mean capture efficiency and compare it to 90%; if the lower limit exceeds 90%, the statement can be made that the average efficiency exceeds 90% with 95% confidence.

The steps to carry out the analysis include:

1. Calculate the average (AVG) and standard deviation (STD) of the n efficiency values where n=number of independent observations
   
   
2. Calculate the degrees of freedom = n-1 and determine the 95^th percentile of the t-distribution with n-1 degrees of freedom (i.e., t0.95, df=n-1)
   
   
3. Calculate the lower bound:
   
   (Equation A-3)
   
   L = AVG – (STD/sqrt(n))× t(0.95, df=n-1)
   
   
4. If the value L is greater than 90% then the system meets the 90% efficiency criterion.

In step 2, the 95^th percentile can be obtained using a published table of t-distribution critical values or by using the “tinv(p,df)” function available in Microsoft EXCEL. The “tinv” function returns the two-tailed inverse of the t-distribution, so care must be exercised in specifying the parameters. The first parameter is the sum of the upper and lower tail probabilities (so for the 95% percentile, use p=0.05+0.05=0.1); the second parameter is the number of degrees of freedom (i.e., df=n-1).

Microsoft EXCEL can be used to analyze the tracer gas data, as illustrated with the following example data.

Example: Suppose that five tests are done and the five example data efficiencies are 93, 93, 94, 95, and 95. These are hypothetical values for the purpose of demonstrating the calculations. Using Equation A-3:

1. The average is 94 and the standard deviation is 1.
2. The degrees of freedom is 5-1=4 and the t-value is 2.132 (obtained in Excel by specifying tinv(0.1,4)).
3. The square root of 5 is 2.236 and the lower bound L=94-(1/2.236)×2.132=93.05.
4. Because L exceeds 90%, the statement can be made that the efficiency is greater than 90% at the 95% confidence level.

The sample calculation is shown using Microsoft EXCEL in Table A-1 to show equations and Table A-2 to show results.

Table A-1. Microsoft Excel example equations for determining L

	A	B
1	Trial	Capture efficiency
2	1	0.93
3	2	0.93
4	3	0.94
5	4	0.95
6	5	0.95
7	Number of trials (N)	5
8	average	=AVERAGE(B2:B6)
9	standard deviation	=STDEV(B2:B6)
10	confidence level	0.95
11	L	=B8-B9/SQRT(B7)*TINV(((1-B10)*2),(B7-1))

Table A-2. Microsoft Excel example results for determining L

	A	B
1	Trial	Capture efficiency
2	1	93%
3	2	93%
4	3	94%
5	4	95%
6	5	95%
7	Number of trials (N)	5
8	average	94.0%
9	standard deviation	0.01
10	confidence level	95%
11	L	93.05%

References

ACGIH [2007]. Industrial ventilation: a manual of recommended practice for operation and maintenance. Cincinnati, OH: American Conference of Governmental Industrial Hygienists.

ACGIH [2013]. 2013 TLVs and BEIs: threshold limit values for chemical substances and physical agents and biological exposure indices. Cincinnati, OH: American Conference of Governmental Industrial Hygienists.

Agresti A, and Franklin C [2009]. Statistics: The art and science of learning from data, 2^nd edition. Pearson. p. 378.

CGA [2008]. Safe handling of compressed gases in containers. 11^th edition. Chantilly VA: Compressed Gas Association.

NIOSH [1973]. The industrial environment—its evaluation and control. Cincinnati, OH: U.S. Department of Health, Education, and Welfare, Center for Disease Control, National Institute for Occupational Safety and Health, pp. 101-122.

NIOSH [1997]. Engineering control guidelines for hot mix asphalt pavers. Cincinnati, OH: Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, DHHS (NIOSH) Publication No. 97-105.

NIOSH [2011a]. A laboratory evaluation of capture efficiencies of the vacuum cutting system on a Wirtgen W 250 cold milling machine at Payne & Dolan Inc., Racine, Wisconsin. By Hammond DR, Trifonoff N, Shulman SA. Cincinnati, OH: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, EPHB Report No. 282-19a [http://www.cdc.gov/niosh/surveyreports/pdfs/282-19a.pdf].

NIOSH [2011b]. Dust-control technology for asphalt-pavement milling controlled-site testing at State Highway 47, Bonduel, Wisconsin. By Hammond DR, Blade LM, Shulman SA, Zimmer J, Cecala AB, Joy GJ, Lo LM, Chekan GJ. Cincinnati, OH: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, EPHB Report No. 282-18a [http://www.cdc.gov/niosh/surveyreports/pdfs/282-18a.pdf].

NIOSH [2012]. A laboratory evaluation of a local exhaust ventilation system on a Caterpillar cold milling machine at Caterpillar, Minnesota. By Hammond DR, Garcia A, Henn S, Shulman SA. Cincinnati, OH: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, EPHB Report No. 282-22a [http://www.cdc.gov/niosh/surveyreports/pdfs/282-22a.pdf].

NIOSH [2013]. A laboratory evaluation of a local exhaust ventilation system on a Roadtec cold milling machine at Roadtec, Chattanooga, Tennessee. By Hammond DR, Garcia A, Shulman SA. Cincinnati, OH: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, EPHB Report No. 282-21a [http://www.cdc.gov/niosh/surveyreports/pdfs/282-21a.pdf].

Appendix B: Field Test Procedures

Field testing of the asphalt milling machines should be done after laboratory tracer gas tests of the ventilation controls show greater than 90% capture efficiency. The purpose of field testing is to provide information to the milling machine manufacturer about the performance of their engineering controls on typical highway construction sites. Asphalt milling machine manufacturers need reliable air sampling data for crystalline silica exposures to confirm the effectiveness of the engineering controls before those controls are placed on an entire fleet of milling machines. The procedure outlined in this appendix can also be used to verify the effectiveness of the overall respirable crystalline silica control strategy, which may include any combination of water sprays, ventilation, or other control methods.

Site Selection Considerations

Selected sites should be representative of typical asphalt pavement milling jobs in highway construction. To provide a rigorous test of the milling machine dust controls, manufacturers should consider the following parameters when selecting from a population of typical highway construction study sites for collecting air samples during asphalt pavement milling:

• Consider selecting sites where the milling crew will be working at least an 8-hour shift and less than 30% of the shift is spent on unexpected downtime (e.g., unusually long dump truck delays, milling machine repairs, and weather delays). Expected downtime such as refilling the milling machine with water, replacement of cutting teeth, switching between dump trucks when a truck is fully loaded with recycled asphalt pavement, and minor traffic delays are all typical to asphalt pavement milling and should not be considered as unexpected downtime.
• Do not select sites where more than half of the sample time includes milling around manhole covers and/or within busy intersections.
• Do not conduct air sampling in the rain or when the pavement is still wet from rain.
• Consider finding additional test sites if the average wind speed over any evaluated shift is greater than 5 m/s (11 mph).
• Consider finding additional test sites if the average crystalline silica content in the bulk material is less than 5%.
• Document other potential silica dust sources on or near the site, such as other milling machines without ventilation controls, soil stabilization, and farming operations. Sites should not be excluded based on the presence of other dust sources, but noting their presence may be useful when interpreting results.

Study Design and Data Collection

To field test the effectiveness of dust controls on asphalt pavement milling machines, personal breathing zone air samples of the pavement milling machine operator and a ground person should be analyzed for respirable crystalline silica. The air sample should be collected during a full shift of normal employee work activities. The workers’ arithmetic mean exposures will be compared to the exposure limit. Crystalline silica exposures will be considered acceptably controlled if the upper 95% confidence limit for the arithmetic mean exposure associated with a randomly chosen day at a randomly chosen site is less than the exposure limit (e.g., 0.05 mg/m³ for the NIOSH REL). Because the exposure data are typically log-normally distributed, the estimated log scale means and standard deviations are needed to get upper confidence limits (UCL) for the arithmetic means (AM).

Sampling should be conducted on each of the two workers (operator and ground person) using one of the following two sampling strategies:

1. Sample three days at a minimum of three different milling sites (at least nine sampling days). If additional sites are added, three sampling days should be conducted at each additional
   site.
2. Sample one day at a minimum of five sites.

The statistical methods proposed here work best if a) the same individual does the job at each site or b) different workers do the job at different sites. This applies for both the operator and ground person.

Selection of the sampling strategy should be based on several considerations, including availability of suitable sampling sites, site-to-site variability, and within-site variability. The first strategy, sampling for three days at a minimum of three sites (at least nine sampling days), would be preferred if within-site variability is a major concern. The second sampling strategy, one sampling day at a minimum of five sites, would be preferred if the site-to-site variability is of primary concern. Availability of suitable sites, such as milling sites large enough to support three days of sampling, will also need to be factored into the sampling strategy decision.

Exposure concentrations should be compared against occupational exposure limits for respirable crystalline silica, such as the NIOSH REL of 0.05 mg/m³, the ACGIH TLV of 0.025 mg/m³, and the OSHA PEL. The exposure assessment should be performed by a safety and health professional familiar with the practice of industrial hygiene.

Air sampling should include time-integrated cyclone-filter-pump samples for assessment of workers’ full-shift, time weighted average (TWA), personal breathing zone exposures to respirable crystalline silica. NIOSH has conducted this testing using BGI model GK2.69 cyclones (BGI Inc., Waltham, MA) at a flow rate of 4.2 liters/minute (L/min) with battery-operated sampling pumps. Sampling pumps should be calibrated before and after each day’s use. The 4.2-L/min cyclone is suitable for this application because it should allow for a minimum detectible concentration of about 5% of the REL (10% of the TLV), assuming a 5-μg/sample laboratory limit of detection for quartz and an 8-hour sample time. Other cyclones operating at lower flow rates may not be suitable for this testing because of their higher minimum detectable concentrations.

A sampling pump should be clipped to each sampled employee’s belt, worn at their waist. The pump should be connected via Tygon^® tubing and a tapered Luer-type fitting to a pre-weighed, 37-mm diameter, 5-micron (μm) pore-size polyvinyl chloride filter supported by a backup pad in a three-piece filter cassette, sealed with a cellulose shrink band (according to NIOSH Methods 0600 and 7500) [NIOSH 1998, 2003]. The front portion of the cassette is removed and the cassette is attached to the BGI respirable dust cyclone.

Start and stop times for the sampling pump should be noted. This would include any time when the worker needed to remove the sampler, such as during lunch breaks. Significant events such as process upsets or sampling equipment failures should also be noted. However, pumps should not be stopped for normal delays that are common in asphalt pavement milling such as refilling the milling machine with water, replacement of cutting teeth, switching between dump trucks when a truck is fully loaded with recycled asphalt pavement, short breaks for workers to rehydrate, and minor traffic interruptions or delays.

Bulk samples of the asphalt pavement material should be collected. Collecting bulk samples is important to determine the percent silica in the asphalt pavement being milled, which will then be compared to the percent silica in the filter samples.

Filters should be analyzed gravimetrically for all respirable particulate using NIOSH Method 0600 and then by X-ray diffraction (XRD) for respirable crystalline silica using NIOSH Method 7500 [NIOSH 1998, 2003]. Bulk samples should be analyzed in accordance with NIOSH Method 7500. Analysis should be conducted by an AIHA-accredited laboratory.

Wind velocity, temperature, and humidity should be recorded continuously on-site during sampling. These data can be measured and recorded using any of a number of commercially available weather stations. It is important to locate the wind instrumentation in a location where the readings will not be influenced by passing traffic. It is also possible to use historical weather observations from the National Oceanic and Atmospheric Administration (NOAA) fixed weather station nearest to each evaluated site.

Data Analysis

The testing goal is to obtain an upper 95% confidence limit for the arithmetic mean exposure associated with a randomly chosen day at a randomly chosen site. If this upper 95% confidence limit is less than the occupational exposure limit then the exposures are said to be acceptably controlled. The exposure limit discussed here is the NIOSH REL, 0.05 mg/m³.

Lognormality is typically assumed for exposure data. Lognormality means that the natural logarithms of the measurements approximately follow a normal distribution. The statistical literature provides a variety of methods for estimating an upper confidence limit for the arithmetic mean of a lognormal distribution. The method used here will be presented in two versions to correspond to the two proposed sampling strategies.

An Excel spreadsheet was developed so that manufacturers can analyze their own data to determine the level of dust control (“mover_upper_confidence_limits.xlsx”).

Sampling Strategy 1

With sampling strategy 1, personal breathing zone air samples for respirable crystalline silica are collected for three days at each of three or more sites (ideally four or more).

The statistical method used for the analysis is the “MOVER” method which stands for “Method of Variance Estimates Recovery”. The MOVER method can be used for the balanced design (i.e., same number of days at each sampled site) but can also be used for the unbalanced design (i.e., different number of days at each sampled site). The MOVER method estimates the upper confidence limit (UCL_M) using an approach developed by [Zou et al. 2009].

Analysis of balanced data collected under sampling strategy 1 can be completed in the “Ex. Strategy 1-Balanced” worksheet of the attached Excel spreadsheet.

In the worksheet each measurement is converted to the natural log scale, and the mean for each job category (operator or ground person) is computed for each site. Use of the spreadsheet is described in Appendix D. The following quantities are computed in the spreadsheet: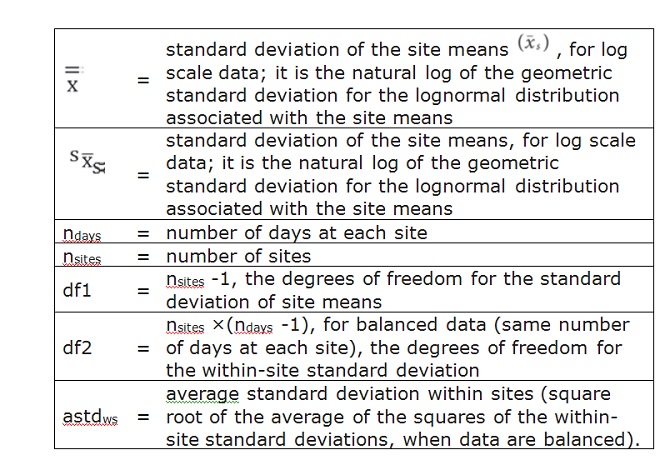

Exponentiating this value gives the within-site (or between days) geometric standard deviation.

To calculate the 95% upper confidence limit, first calculate UCL2, given by:

In equation (B-1), t(0.95,df1) is the 95^th percentile of the t distribution with df1 degrees of freedom and chisq(1-0.05,df2) denotes the 95^th percentile of the chi square distribution with df2 degrees of freedom.

Then the 95% upper confidence limit is given by

UCL_M=e^UCL2 (Equation B-2)

This limit is discussed in more detail in Appendix C. Simulations in that section indicate that for most parameter values studied, the coverage for the method is close to the nominal 95%.

Analyses of Example Data

The following example data in Table B-1 are also in the “Ex. Strategy 1-Balanced” worksheet of the spreadsheet. For simplicity, the example considers three days of sampling at each of three sites rather than the recommended four sites. These are hypothetical values for the purpose of demonstrating the calculations.

Table B-1: Example data for 3 days per site at 3 sites

Site	Day	Groundperson silica concentration (mg/m3)	Ln (Ground person silica concentration)	Ground person site means, Ln scale		Within- site standard deviation, Ln scale
1	1	0.00507	-5.284	-5.645		0.354*
1	2	0.00349	-5.658
1	3	0.00250	-5.992
2	1	0.01200	-4.423	-5.172		0.692
2	2	0.00308	-5.787
2	3	0.00495	-5.308
3	1	0.01010	-4.595	-4.565		0.476
3	2	0.00575	-5.159
3	3	0.01480	-4.213
			= mean(site means) =	-5.158	astdws=average standard dev. (within-site)=	0.526**
			= standard dev.(site means) =	0.495***
		df1	= degrees of freedom=nsites-1 =	2
	* 0.354 is the standard deviation of (-5.284,-5.658,-5.992). ** It is customary to average the variances, which are the squares of the standard deviations. The average within-site variance is 1/3 x (0.3542 + 0.6922 + 0.4762)=0.277, the square root of which is 0.526. However, in the spreadsheet, the calculations use a more general form also applicable to unbalanced data: multiply each within-site variance by its degrees of freedom, ndays-1. Divide the sum of the weighted variances by the sum of the degrees of freedom: (2×0.3542 + 2×0.6922 + 2×0.4762)/(2+2+2)=0.277. *** 0.495 is the standard deviation of (-5.645,-5.172,-4.656).

The between-site standard deviation is given by 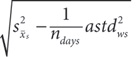= sqrt(0.4952-0.3333×0.5262)=0.391.

Consequently, the within-site GSD is exp(0.526) = 1.692 and the between-site GSD is exp(0.391) = 1.48. Also, the GM is exp()=exp(-5.158)=0.0058, where “exp” denotes the exponential function.

From equation (B-1), UCL2 = (Term1 + sqrt (Term2 + Term3 + Term4)).

Where:

• Term1 = 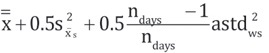. Using values from Table B-1, Term1 = -5.158 + 0.5 x (0.495² + 2/3 x 0.526²) = -4.9433. (The total ln scale variance is 0.495² + 2/3 x 0.526²=0.429, which corresponds to a total ln scale standard deviation of √0.429=0.655. The total geometric standard deviation is e^√0.429 =1.925. Also, note that the fraction of total variance due to sites is 0.391²/0.429=0.36, where 0.391 is the between-site standard deviation.)
  
• Term2 = 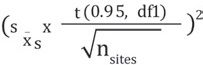uses the upper confidence limit for the mean. Using values from Table B-1, Term2 = (0.495² x 2.920²/3) = 0.6958, where df1 = n_sites-1 = 3-1 = 2 and 2.920 is the 95^th percentile of the t distribution with 2 degrees of freedom.
• Term3 =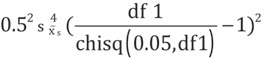uses the upper confidence limit for the between-site variance. Using values from Table B-1, Term3 = 0.5² x 0.495⁴ x (2/0.1026-1)² = 5.125, where df1 = n_sites-1 = 3-1 = 2 and 0.1026 is the 5^th percentile of the chi square distribution with 2 degrees of freedom.
• Term4 =uses the lower confidence limit for the average of the within-site variances (the reason for this is discussed in Appendix C). Using values from Table B-1, Term4 = 0.5² x 0.667² x 0.526⁴ x (6/12.592-1)² = 0.0023, where df2 = n_sites (n_days-1) = 3(3-1) = 6, and 12.592 is the 95^th percentile of the chi square distribution with 6 degrees of freedom.

Substituting these values into equations (B-1) and (B-2), gives UCL_M=exp(-4.9430 +sqrt(0.6958+5.125+0.0023))=0.0797 mg/m³.

Thus, for the example data, the 95% upper confidence limit for the arithmetic mean for the ground person exceeds the NIOSH REL of 0.05 mg/m³.

Unbalanced Data

When the number of days at each site is not the same, many of the terms in equation (B-1) remain the same; however, there are four important changes. Using the notation of [Krishnamoothy 2014]: is still the average of the site means, is still the variance of the site means about and df1 is still (n_sites-1). The four changes are:

1. df2= (number of measurements)-(number of sites)
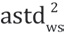2. is the sum of the weighted within-site variances divided by df2. Each weight is the number of days at the site minus 1. For instance, if there are 3 days at sites one and two and 2 days at the third site, the weights are, respectively, 2 and 2 and 1.
3. In equation (B-1), ((n_days-1)/(n_days)) is replaced by (1-nbar), where nbar is the average of the reciprocals of the number of days at the sites. For the example in (2) above, nbar = (1/3+1/3+1/2)/3 = 0.389. Thus, (1-nbar) = 1-0.389 = 0.611.
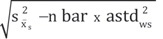4. = standard deviation between sites; note that for balanced data, nbar=1/n_day.

Analyses of Unbalanced Example Data

The data are shown in the worksheet “Ex. Strategy 1-Unbalanced”. For the data used above, the measurement for site 2, day 3 has been omitted.

First, when the data are unbalanced, the squared within-site standard deviations must be weighted by their degrees of freedom. For the ground person data, the weights for the three within-site variances are 2, 1, and 2:

astd_ws = sqrt[(2x0.12539 + 1x0.9292 + 2x0.2262)/(2+1+2)]

= sqrt[(0.2508 + 0.9292 + 0.4524)/5]=0.5714.

Second, the other important differences from the balanced case are due to the unequal number of days at each site. Let nbar=0.389, as was explained above. In equation (B-1), the term ((n_days-1)/(n_days)) is replaced by 1-nbar=1-0.389=0.611. Also, df2=8-3=5, since there are eight measurements and 3 sites.

Also, = standard deviation between sites =
sqrt(0.4953²-0.389×0.5714²)=0.3440.

With these changes, the results are:

• Term1 = 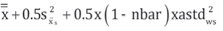= -5.1349 + 0.5 x (0.4953² + 0.611 x 0.5714²) = -4.9125. (The total ln-scale variance is 0.4953² + 0.611 x 0.5714²=0.445, which corresponds to a total ln-scale standard deviation of √0.445=0.667. The total geometric standard deviation is e^√0.445 =1.95.)
• Term2 = 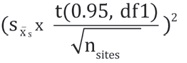= (0.4953 x 2.920/sqrt(3))² = 0.6972.
• Term3 = 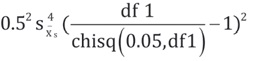= 0.5² × 0.4953⁴ × (2/0.1026 -1)² = 5.146.
• Term4 =
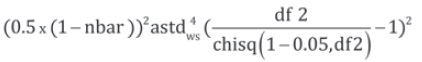
  = 0.5² x 0.611² x 0.5714⁴ x (5/11.0705 -1)² = 0.002992, where 11.0705 is the 95^th percentile value of the chi square distribution with 5 degrees of freedom.
• UCL_M = exp(-4.9125 + sqrt(0.6972 + 5.146 + 0.002992)) = 0.0825 mg/m³.
• For both occupations the limits increase slightly when the third day at site 2 is omitted.

Conclusions from Data Analysis

As shown in the “strategy 1-balanced” worksheet, the 95% upper confidence limit for the operator is 0.177 mg/m³. Thus, for analysis of the full example data set at the 95% confidence level, it cannot be concluded that the exposures are controlled below the NIOSH REL of 0.05 mg/m³. This conclusion applies to the population of sites from which the sample sites were drawn, with 95% confidence for each job category, or 90% overall confidence for both job categories (operator and ground person).

If the upper confidence limits are above the NIOSH REL, this means one of two things, either (a) the population mean is above the REL and the dust control system is not capable of reducing exposures below the REL, or (b), the population mean is below the REL, but the sample size (3 days of sampling at each of 3 sites) does not permit a precise estimate of the population mean.

There is some additional discussion in the “Design Considerations” section after the discussion of sampling strategy 2.

Sampling Strategy 2

An alternative collection strategy involves sampling at five or more sites with one day per site.

Analysis of the data is done in the Excel spreadsheet with the worksheet name “Ex. Strategy 2”. For sampling strategy 2, a minimum of five sites should be sampled, with only one day of sampling at each of the five sites.

UCL2=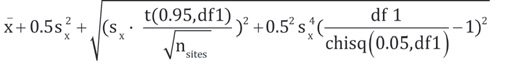(Eq B-3)
where

• df1=n_sites-1,
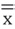• is the natural log scale mean,
• is the natural log scale variance, df1 is n_sites-1,
• t(0.95,n_sites - 1) is the 95^th percentile of the t distribution with df1 degrees of freedom, and
• chisq(0.05,df1) is the 5^th percentile of the chi square distribution with df1 degrees of freedom.
  

UCL_M = e^UCL2 (Equation B-4)

The following example data in Table B-2 are in the “Ex. Strategy 2” worksheet of the spreadsheet. These are hypothetical values for the purpose of demonstrating the calculations.

Table B-2: Example data for one day at five sites

Site	Day	Ground person silica concentration (mg/m3)	ln (ground person silica concentration)
1	1	0.005	-5.298
2	1	0.012	-4.423
3	1	0.010	-4.605
4	1	0.008	-4.828
5	1	0.006	-5.116
		= mean(sites) =	-4.854
		= standard deviation(sites) =	0.359
		df1 = Degrees of freedom = nsites-1	4

From equation (B-3), UCL2 = Term1 + sqrt (Term2 + Term3).

Where:

• Term1= = -4.854 + 0.5 x 0.359² = -4.789.
• Term2= 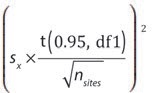= (0.359 × 2.1318/sqrt(5))² = 0.1169, where 2.1318 is the 95^th percentile of the t distribution with 4 degrees of freedom.
• Term3= 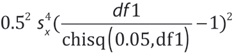=0.25×0.359⁴×(4/0.7107- 1)²=0.0886, where 0.7107 is the 5^th percentile of the chi square distribution with 4 degrees of freedom.

Finally, UCL2 = (-4.789 + sqrt(0.1169+0.0886)) = -4.335 and UCL_M = e^UCL2 = exp(-4.335) = 0.0131 < 0.05 mg/m³.

Thus, at the 95% confidence level, it can be concluded that the exposures for the job category are less than the NIOSH REL of 0.05 mg/m³ for the data in this example. The corresponding upper confidence limit for the operator is 0.024 mg/m³, as shown in the example worksheet, to which the same conclusion applies. Thus, these conclusions apply to the population of sites from which the sample sites were drawn, with 95% confidence for each job category, or 90% overall confidence for both job categories (operator and ground person) for the example data.

Study Design Considerations

Important issues are the choice of strategy 1 or strategy 2, and, for either strategy, the number of sites to select. Given the cost associated with moving the milling machine to each site, using fewer sites may result in cost savings for the testing. Using too few sites, however, could result in low statistical power, which is the probability of correctly identifying an arithmetic mean below the occupational exposure limit. For the purposes of this document this is the probability that the 95% upper confidence limit is less than the NIOSH REL of 0.05 mg/m³. General guidelines for choosing the sampling strategy were provided in Appendix B. More detailed calculations for determining sampling strategy are provided here.

Tables C-2, C-5, and C-6 in Appendix C give the power (estimated using statistical simulation) for various geometric means (GMs) and geometric standard deviations (GSDs). Table C-2 is for strategy 2, one day at each site; Table C-5 is for strategy 1, three days at each site. The GMs considered are 0.006, 0.01, and 0.025 mg/m³ (all less than the NIOSH REL). The 0.006 mg/m³ value is based on two past studies [NIOSH 2013a,b]; the 0.025 mg/m³ value was added to see how large the GM can be and still have sizable power. The total GSDs from past studies varied between about 1.7 and 1.9 [NIOSH 2013a,b]; Table C-5 shows power results for total GSD 1.92, and Table C-6 shows results for a wider range of total GSDs, but only for GMs 0.006 and 0.01 mg/m³.

The results in the Appendix C tables indicate that if the between-site variance is much larger than the within-site variance, little is gained in terms of power by sampling more than one day at each site. For example, for a GM of 0.006 mg/m³ and a total GSD of 1.92, the power of strategy 2 (Table C-2) with 5 sites is 82.2% whereas the power of strategy 1 with 5 sites when most of the variability is between-sites is 84.7% (Table C-5). Thus strategy 2 is preferable because there is no real benefit to the extra work of collecting three days of data at each site. However, if the within-site variance is larger than the between-site variance, then sampling more than one day at each site will increase the study power (e.g., for a GM of 0.025 mg/m³ and a total GSD of 1.92, the power of strategy 2 with 5 sites is 23.0% (Table C-2), but increasing the number of sampling days at each site from 1 to 3 increases the study power to around 48% when most of the variability is within-site (Table C-5)). Thus, strategy 1 would be preferred over strategy 2 for this example. This is a general conclusion of the effect of large versus small between-site variance that applies whenever the comparison between strategies is made for the same number of sites for the two strategies. The problem is that there is no way to know whether between or within- site variance is larger without collecting data, and, it is expensive to do a preliminary study to provide information about this question.

Based on the data available in two NIOSH reports [NIOSH 2013a,b] the recommendation is to use one of the following options:

Strategy 1: Use four sites, with three days per site. From Table C-6, for a total GSD of about 1.92, the power is between 66% and 94% for a GM of 0.006 mg/m³. From two past NIOSH reports, 0.006 mg/m³ is an attainable value [NIOSH 2013a,b]. If the GSD is about 2.25, the power is between 46% and 79% for GM 0.006 mg/m³. For each interval, as explained above, the lower values (66% and 46%) are at the highest between-site variance shown.

Strategy 2: Use five sites, with one day per site. For GSD of about 1.9, the power is 82% and for GSD 2.25 the power is 61%, both for GM 0.006 mg/m³ (Table C-2).

Both strategies offer reasonably high power (minimum close to 50% and maximum at least 80%) even if the total GSD is somewhat larger than that observed in past studies (GSD 1.92). Because of limited information about the between-site variance, there is no way to know beforehand which design is preferable. If the GM is 0.01 mg/m³, for GSD 1.92, both strategies still have at least 50% power.

If the strategy 1 and 2 options above are impractical, there is an option with less power:

Strategy 1, 3 sites: Use three sites, with three days per site, with the understanding that although this design lacks power, it could still work under some conditions. The power is between 39% and 67% for a GSD of 1.92 and a GM of 0.006 mg/m³ and between 28% and 49% for a GSD of 2.25 and GM of 0.006 mg/m³ (Table C-6). The lower values are at larger between-site variance and the higher values are at lower between-site variance. Note that this is clearly inferior in power to the four site strategy 1 design results given above.

These recommendations are based on the observation that the total GSD from two past studies did not exceed 1.9 [NIOSH 2013a,b]. It is possible that future studies could result in larger GSDs that would require more sites to offer sufficient power, under either strategy, but this can only be determined when future results are obtained. If GMs are low, for example 0.01 mg/m³ or less, but the upper confidence limits exceed the REL, this indicates lack of sufficient statistical power for the obtained GSDs. The power results in Tables C-2 and C-6 can help determine the number of sites required in a follow-up study to achieve adequate power for some larger GSDs. Note that it is imperative to decide beforehand on the sample size and not change the sampling plan after starting to collect and analyze data. Thus, if after collection of data it seems that more sites should have been sampled, a new study must be done using the revised number of sites.

Additional Comments

1. During data analysis, there may be situations where a sample value is missing (due to a sampling problem), unknown (perhaps because the sample determination is less than the limit of detection), or determined to be an outlier. When a sample is missing because of a sampling problem or excluded as an outlier the MOVER method can be used without the missing (or excluded) sample result. When a measurement is unknown because the determination is less than the limit of detection (LOD), a choice must be made among the following substitution procedures. It is not appropriate to exclude the unknown measurement in this case. If there is more than one value below the LOD, a statistician should be consulted; however, when there is just one such value, a simple method is to replace a single value below the LOD with the limit of detection divided by the square root of 2 [Hornung and Reed 1990].
2. The statistical methods proposed here work best if a) the same individual does the job at each site or b) different workers do the job at different sites. This applies for both the operator and ground person. If other arrangements are used, a statistician should be consulted.
3. The Excel worksheets in the spreadsheet “mover_upper_confidence_limits.xlsx” are provided so that the users of this document can enter their data into the appropriate sheet, and obtain 95% upper confidence limits for the arithmetic means of their data. See Appendix D for directions for using the spreadsheet.
4. The Silica/Asphalt Milling Machine Partnership recommends that asphalt milling machine manufacturers implement dust controls capable of reducing worker exposures below the NIOSH REL for respirable crystalline silica of 0.05 mg/m³ at the 95% confidence level. Several asphalt milling machine manufacturers have also developed their dust controls to reduce worker exposures below the ACGIH TLV value for respirable crystalline silica of 0.025 mg/m³. The upper confidence limits provided in this document and in the spreadsheet can be used for comparison to either occupational exposure limit.
5. In the methods presented here, each job category is evaluated separately, so that the results apply individually at the 95% confidence level and for both job categories with about 90% confidence.
6. Field data may include outliers. There are statistical methods for identifying outliers. Table B-3 contains 99% limits for the Grubbs statistic for a single upper outlier. For the natural log scale data, the calculated value
   
   g = [(maximum- mean)/ standard deviation]
   
   should be compared to the applicable Grubbs statistic, and if the value exceeds the 99% value in Table B-3, that data point could be removed. However, it is always important to have a reason based on some peculiarity of the particular sample to justify removing the data point. The formula can be used as follows:
   • For either sampling strategy 1 or 2, the value of n should be the number of sites. For sampling strategy 1 the “maximum” is the largest site mean, the “mean” is the mean (site means), and the “standard deviation’ is the standard deviation (site means). For sampling strategy 2 the “maximum” is the largest site measurement, the “mean” is the mean(sites) and the “standard deviation” is the standard deviation(sites). For example, from Table B-2, the maximum log scale site measurement is (-4.423) where n=5 and g=(-4.423-(-4.854))/0.359=1.201. From Table B-3 the 99^th percentile of the Grubbs statistic for n=5 is 1.75. Because 1.201 < 1.75, there is no reason to consider the largest measurement to be an outlier.
   • For sampling strategy 1, an additional use of the formula can be made for evaluation at a particular site where n=the number of days at the site=3. The “maximum” is the largest measurement for the site, the “mean” is the mean for the site, and the “standard deviation” is the standard deviation for the site. If multiple sites are tested, this application should only be performed in consultation with a statistician, because of complications that involve use of multiple tests.
   • The g test can be performed with either the maximum or the minimum, whichever is considered a possible outlier. Use of the minimum will result in a negative value. To determine whether the minimum is a possible outlier, change the sign to positive and compare to the value in Table B-3 for the given n value.

Table B-3. 99% values for Grubbs test for a single upper outlier. [Barnett and Lewis 1978]

n*	99% value
3	1.15
4	1.49
5	1.75
6	1.94
7	2.10
* For sampling strategy 1, “n” = nsites when determining if a site mean is an outlier compared to the other site means and “n” = ndays when determining if a within-site test result is an outlier compared to other site-specific results. For sampling strategy 2, “n” = nsites.

References

Barnett V, and Lewis T [1978]. Outliers in statistical data. New York: Wiley, p. 298.

Hornung R, Reed L [1990]. Estimation of average concentration in the presence of nondetectable values. Appl Occup Environ Hyg 5(1):46–51.

NIOSH [1998]. Particulates not otherwise regulated, respirable. In: Schlecht PC, O’Connor PF, eds. NIOSH manual of analytical methods (NMAM). 4th ed. 2nd supplement. Cincinnati, OH: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, DHHS (NIOSH) Publication No. 98-119.

NIOSH [2003]. Silica, crystalline, by XRD (filter redeposition). In: Schlecht PC, O’Connor PF, eds. NIOSH manual of analytical methods (NMAM). 4th ed. 3rd supplement. Cincinnati, OH: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, DHHS (NIOSH) Publication No. 2003-154.

NIOSH [2013a]. Control technology for crystalline silica exposure during pavement milling using a Roadtec milling machine equipped with a local exhaust ventilation system. By Hammond DR, Shulman SA Cincinnati, OH: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, EPHB Report No. 282-25a [http://www.cdc.gov/niosh/surveyreports/pdfs/282-25a.pdf].

NIOSH [2013b]. Control technology for crystalline silica exposure during pavement milling using a Wirtgen milling machine equipped with a vacuum cutting system. By Hammond DR, Shulman SA. Cincinnati, OH: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, EPHB Report No. 282-23a [http://www.cdc.gov/niosh/surveyreports/pdfs/282-23a.pdf].

Zou, G.Y., Taleban, J., and Huo, C.Y. [2009]. Confidence interval estimation for lognormal data with applications to health economics. Computational Statistics and Data Analysis. 53: pp. 3755-3764.

Appendix C: Explanation of Statistical Methods

The criterion used for evaluating the dust control strategy is that the arithmetic mean of the exposure measurements for a randomly chosen day at a randomly chosen site should be less than the occupational exposure limit (here the NIOSH REL of 0.05 mg/m³ is used). This will be assessed by obtaining an upper 95% confidence limit for the arithmetic mean. If this upper 95% confidence limit is less than the occupational exposure limit then the exposures are said to be acceptably controlled.

Two sampling strategies are considered: 1) multiple sites (at least three), with three sampling days at each site and 2) multiple sites (at least five), with one sampling day at each site.

Under sampling strategy 1, for each of the two job categories the data are treated as coming from a one-way random effects model on the natural log scale:

x_sd= μ + a_s + b_d(s), (Equation C-1)

where “s” indexes the sites, “d(s)” indexes the days at the sites, x_sd is the natural logarithm of the sampling result at site “s” on day “d”, and μ is the mean on the natural log scale (i.e., the natural log of the geometric mean(GM)). Site is treated as a random effect (a_s) which is normally distributed with mean 0 and between-site variance σ²_s (on the natural log scale). The days at each site are also treated as random (error) which is normally distributed with mean 0 and days within-site variance σ²_d(s) (on the natural log scale). The arithmetic mean is given by exp(μ + 0.5(σ²_s + σ²_d(s))).

Under sampling strategy 2, the model simplifies to:

x_s= μ + a_s, (Equation C-2)

where “s” indexes the sites, x_s is the natural logarithm of the sampling result at site “s”, and μ is the mean on the natural log scale (i.e., the natural log of the GM). Site is treated as random (error) which is normally distributed with mean 0 and between-site variance σ²_s (on the natural log scale). In this scenario the arithmetic mean is given by exp(μ + 0.5(σ²_s)).

In the following, methods are given for estimating the 95% upper confidence limit of the arithmetic mean. Simulation results will be provided a) to evaluate the coverage of the proposed methods for a wide range of possible parameter values and b) to give an idea of the power of the methods based on estimated means and variances from past data. Sampling strategy 2 is discussed first, because it is simpler.

Sampling Strategy 2

Here, the goal is to estimate a 95% upper confidence limit for the arithmetic mean, exp(μ + 0.5(σ²_s)). There are exact confidence limits for the lognormal mean based on Land’s coefficients [Gibbons and Coleman 2001] and [Land 1972], when the data are a simple random sample. However, this approach requires using tables that depend on the number of sites, thus requiring separate work sheets for each possible sample size. Instead, an approach is presented here that can be programmed in a single worksheet. The MOVER approach described by [Zou et. al. 2009] is used to obtain an upper confidence limit for μ + 0.5(σ²_s) and this result is exponentiated to obtain an upper confidence limit for the arithmetic mean.

According to [Zou et. al. 2009], for unbiased, statistically independent estimators ,, with 95% upper confidence limits u₁, u₂, an upper 95% confidence limit for the linear combination is:

.

In this application, θ₁ is the natural log scale mean, θ₂ is the natural log scale variance, a₁=1 and a₂=0.5. In the formulation of [Zou et. al. 2009], the required upper confidence limit for the data described by Equation (C-2) is:

UCL2 = 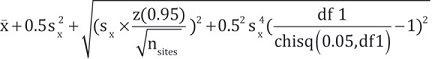(Equation C-3),

where is the natural log scale mean, S_x is the natural log scale standard deviation, z(0.95) is the 95th percentile of the standard normal distribution, df1 = n_sites-1, and chisq(0.05,df1) is the 5^th percentile of the chi square distribution with df1 degrees of freedom.

(The derivation in [Zou et al. 2009] uses the proportionality of the squared differences 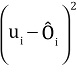to the variance of in large samples to justify the expression UCL2. When independence is lacking, a term for the covariance must be included.)

Because the sampling strategy will likely include a small number of sites, consider a modification that the z value be replaced by the analogous t-distribution value with df1 degrees of freedom, already shown as Equation (B-3):

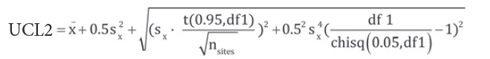
where df1 = n_sites-1 and t(0.95,df1) is the 95^th percentile of the t distribution with df1 degrees of freedom.

For either method, the MOVER upper confidence limit (UCL_M) is obtained by exponentiation of this result, as in Equation (B-4):

UCL_M = e^UCL2 = exp(UCL2).

Statistical simulation was used to compare the coverage of these two methods:

1. Method 1 uses MOVER, as in equation (6) of [Zou et al. 2009] with the 95th percentile of the z (standard normal) distribution for the confidence interval of the mean.
2. Method 2 uses MOVER, but replaces the 95^th percentile of the z (standard normal) distribution with the 95th percentile of the t distribution with k-1 degrees of freedom, where k is the number of sites (one measurement at each site).

For these simulations, the between-site variance (on the natural log scale) was varied from 0.25 to 5 and the population mean μ was set to -0.5σ², where σ² is the log scale variance. (Most of these values were used in [Zou et al. 2009]’s Table 1, although they calculated two-sided 95% confidence intervals, rather than the one-sided 95% upper confidence limits computed in these simulations). In this case, the upper confidence limit is for the arithmetic mean = exp(μ+0.5σ²)=exp(0)=1, or, equivalently, 0 on the natural log scale. By making the arithmetic means the same, the upper confidence limits can be compared for different variance values. The coverage is the percentage of simulations for which the arithmetic mean is less than the upper confidence limit. However, the coverage is not affected by the value of the arithmetic mean. For each combination of k (number of sites) and σ² (between-site variance), 50,000 simulations were performed. The results are described in Table C-1.

Table C-1: Coverage (expressed as percentage) for nominal 95% upper confidence intervals for (natural log scale) arithmetic mean of lognormal data from a random sample of 1 day at each of k sites, by 2 methods.

		k=5 sites		k=6 sites		k=7 sites
GSD+	Log scale variance, σ2s	Method 1 MOVER, Using z statistic	Method 2 MOVER, Using t statistic	Method 1 MOVER, Using z statistic	Method 2 MOVER, Using t statistic	Method 1 MOVER, Using z statistic	Method 2 MOVER, Using t statistic
1.65	0.25	93.4 (0.69)*	95.0 (0.75)	93.0 (0.53)	94.7 (0.58)	93.1 (0.45)	94.6 (0.49)
2.03	0.50	93.7 (1.26)	94.8 (1.33)	93.8 (0.96)	94.8 (1.01)	93.7 (0.795)	94.8 (0.84)
2.72	1	94.3 (2.43)	95.0 (2.49)	94.2 (1.81)	95.0 (1.87)	94.1 (1.47)	94.9 (1.52)
3.40	1.5	94.5 (3.52)	95.2 (3.65)	94.4 (2.65)	95.0 (2.71)	94.4 (2.13)	95.0 (2.19)
4.11	2	94.7 (4.75)	95.2 (4.83)	94.6 (3.48)	95.1 (3.54)	94.6 (2.8)	95.0 (2.85)
4.86	2.5	94.7 (5.91)	95.2 (5.99)	94.9 (4.33)	95.3 (4.39)	94.6 (3.47)	95.0 (3.52)
5.65	3	95.0 (7.06)	95.3 (7.14)	94.9 (5.21)	95.2 (5.28)	94.6 (4.14)	95.0 (4.19)
9.36	5	95.0 (11.69)	95.2 (11.82)	95.0 (8.55)	95.2 (8.71)	94.8 (6.83)	95.0 (6.83)
* Cell entry is the actual coverage (the average value of the upper confidence limit on the log scale is in parentheses). For all simulations, the arithmetic mean converted to the log scale is 0 and there are ndays=1 at each site. Results based on 50,000 simulations. + GSD =

The results show that method 1 using the z percentiles gives coverage less than 95%, especially for the smaller variances. This is consistent with [Zou et al. 2009]’s Table 1, where, for the smaller variances, the coverage of the upper confidence limit for method 1 is less than the nominal value. The use of the t percentiles in method 2 corrects for this. The average value of the upper confidence limits is somewhat larger for method 2, since that method has larger coverage.

Statistical simulation was also used to calculate the power for the MOVER method based on the t-statistic. For the simulations done here the GM of 0.006 mg/m³ was used because it was the overall GM of geometric means from two past studies [NIOSH 2013a,b]. In addition, computations for GMs of 0.01 and 0.025 mg/m³ have been included in the table. Total geometric standard deviation (GSD) for the data from past studies varied between about 1.7 and 1.9. Values of this magnitude as well as those somewhat smaller and somewhat larger were used in the calculations, as shown in the table. If future studies have approximately the specified GMs and GSDs in the range shown in the table, then the probabilities of meeting the REL will be approximately those shown in Table C-2. Coverage is the fraction of simulations such that [ln(GM) + 0.5σ²_s] is less than the 95% upper confidence limit for the MOVER method 2, using the t statistic (Equation (B-3)). Power is the fraction of simulations such that the upper confidence limit for MOVER method 2 will be less than the NIOSH REL of 0.05 mg/m³.

Table C-2: Coverage and power (expressed as percentages) for strategy 2 data, using Mover method 2.*

			5 sites		6 sites		7 sites
GM+	GSD	Log scale variance, σ2s	Coverage	Power	Coverage	Power	Coverage	Power
0.006	1.4	0.11	94.8	100.0	94.6	100	94.5	100.0
	1.75	0.31	94.9	92.5	94.7	98.1	94.9	99.6
	1.92	0.426	94.9	82.2	94.8	92.4	94.6	97.3
	2.25	0.66	95.0	61.1	95.1	74.4	94.7	84.1
	3.0	1.21	95.4	31.4	95.1	39.7	94.9	47.9
0.01	1.4	0.11	94.5	99.9	94.4	100.0	94.6	100.0
	1.75	0.31	94.9	82.1	94.8	92.0	94.6	97.0
	1.92	0.426	95.0	67.6	94.8	81.0	94.7	89.0
	2.25	0.66	95.0	45.1	95.1	56.0	94.9	66.0
	3.0	1.21	95.2	20.6	95.1	26.0	95.3	31.0
0.025	1.4	0.11	94.6	81.0	94.4	91.0	94.7	96.0
	1.75	0.31	94.8	34.0	94.9	42.0	94.4	50.0
	1.92	0.426	94.9	23.0	94.7	28.0	94.8	34.0
	2.25	0.66	95.0	13.0	95.0	15.0	94.7	18.0
	3.0	1.21	95.1	5.8	95.0	6.2	95.1	6.3
* For all simulations, there are ndays=1 at each site. Results based on 50,000 simulations.

The coverage is slightly anti-conservative for the variances shown here, which is consistent with Table C-1 results for method 2 for relatively small variances. In general, the coverage is quite close to 95% for method 2; coverage is never less than 94.4% and never more than 95.4%.

For larger variances, power is much larger when 7 sites are used. However, for the GSD magnitude similar to that in previous studies (1.92), the chances of meeting the REL are quite high (>80%) for 5 sites if the GM is as low as 0.006 mg/m³. For the same GSD and GMs of 0.01 and 0.025 mg/m³, respectively, the power drops to 68% and 23%, respectively.

Sampling Strategy 1 – Balanced Design

The goal is to estimate a 95% upper confidence limit for the arithmetic mean, exp(μ + 0.5(σ²_s + σ²_d(s))), for the data model given by Equation (C-1). Sampling strategy 1 data are not a simple random sample since there are multiple days at each site, so the statistical methods are more complicated. For large samples, the delta method approximation can be used in conjunction with maximum likelihood or ANOVA estimation to calculate confidence levels [Mandel 2013], but the sample sizes here are all small. Therefore, the choice of nominal confidence level for these methods must be calibrated by simulation, because nominal confidence differs from actual confidence. There is an approach based on generalized confidence intervals that can be used, although for small samples it must also be calibrated by simulation [Krishnamoorthy and Mathew 2002]. The work of [Zou et al. 2009], however, can be easily generalized to the case of two variance components, as in [Krishnamoorthy and Peng 2014], equation (2), as follows.

For statistically independent estimators , with 95% upper confidence limits u₁, u₂, and u₃, and 5% lower confidence limits l₁, l₂, and l₃, an upper 95% confidence limit for a linear combination is a₁θ₁+a₂θ₂+a₃θ₃:

where u_i*= u_i if a₁>0, l₁ if a_i<0.

Interest is in estimation of the upper confidence limit for the linear combination

μ + 0.5 (σ²_s + σ²_d(s)) =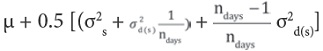

In this application, θ₁ is μ (natural log of the GM); for n_days at each site, θ₂ is the variance of site means for natural log transformed data ; and θ₃ is the within-site variance (σ²_d(s)). Furthermore, all a_i>0 (specifically, a₁=1, a₂=0.5, and for balanced data with n_days at each site, a₃=0.5 x (1-1/n_days)). However, contrary to the assignment rule in [Krishnamoorthy and Peng 2014], simulation results indicate that for the sample sizes of interest in our study, coverage is much closer to nominal when u₃* = l₃. [Krishnamoorthy 2014] recommends this alteration and simulation results are shown below that also support this choice.

Thus, the required upper confidence limits can be obtained as follows:

The sample variance of the natural log scale site means ( in equation B-1) estimates θ₂ and the average within-site variance (denoted astd²_ws) estimates θ₃ = σ²_d(s). Thus, the average of the log scale site means, , and . Upper confidence limits for the corresponding parameters are given by u₁ = t_{(0.95, df1)/}sqrt(n_sites), u₂ = df1× /chisq(0.05,df1 ), and l₃=df2×astd_ws²/chisq(1-0.05,df2), respectively, where astd_ws is the average standard deviation within sites (square root of the average of the squares of the within-site standard deviations for balanced data), df1 = n_sites-1, and (for balanced data) df2 = n_sites x (n_days-1). Also, t(0.95,df1) denotes the 95^th percentile of the t distribution with df1 degrees of freedom; chisq(0.05,df1) denotes the 5^th percentile of the chi square distribution with df1 degrees of freedom; and chisq(1-0.05,df2) denotes the 95^th percentile of the chi square distribution with df2 degrees of freedom. Making substitutions and simplifying yields the required upper confidence limit for balanced data, shown in Equation (B-1):

UCL2=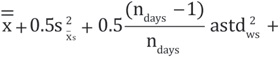

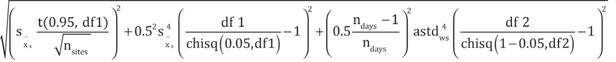
UCL_M=e^UCL2 is the required upper confidence limit, given above in Equation (B-2).

(Equation (B-1) is analogous to Equation (6) of [Zou et. al. 2009].)

Statistical simulation was used to compare the coverage of the two methods:

1. MOVER (using all upper confidence limits), denoted UCL_M,U
2. Modified MOVER (using upper confidence limits, except using the lower confidence limit for the variance between days), denoted UCL_M.

In these simulations, coverage was estimated for several balanced designs (3, 4, or 5 sites) based on 3 days per site. As in Table C-1 the aim is to make the upper confidence limits comparable. Analogous to Table C-1 the value of μ is [-0.5 ×(σ_s² + σ²_d(s))], where σ_s² is the between-site variance and σ²_d(s) is the days within-site variance. For each choice of variances, the upper confidence limit is for exp[μ+0.5×(σ_s² + σ²_d(s))]=exp(0)=1, or, equivalently, 0 on the natural log scale. In Table C-3 seven scenarios for σ_s² and σ²_d(s) were considered, for σ_s² + σ²_d(s)=1 in each scenario. The coverage is evaluated for a very wide range of the ratio of the between-site variance to the total variance, to demonstrate that the coverage is maintained, whatever that ratio is. For each set of parameter values, 50,000 simulations were performed. The coverage is the percentage of simulations for which the arithmetic mean is less than the upper confidence limit. Because the coverage will vary also with the magnitude of the total variance (σ_s² + σ²_d(s)), Table C-4 presents simulations results for other total variance values, using four other variances from Table C-1, just for n_sites equal 3 and 5.

 

Table C-3: Coverage (expressed as percentage) for nominal 95% upper condence intervals for (natural log scale) arithmetic mean of lognormal data for strategy 1 for the two MOVER methods when log scale total variance is 1, and ln (arithmetic mean) =0

			3 sites		4 sites		5 sites
σs2	σ2d(s)	σs2/ (σs2+σ2d(s))	UCLM,U	UCLM	UCLM,U	UCLM	UCLM,U	UCLM
0	1	0	98.2 (3.49)*	95.5 (3.27)	97.8 (1.63)	95.0 (1.43)	97.4 (1.12)	94.5 (0.96)
0.2	0.8	0.2	97.9 (4.62)	95.5 (4.47)	97.3 (2.03)	95.1 (1.92)	96.7 (1.34)	94.8 (1.26)
0.3	0.7	0.3	97.6 (5.20)	95.5 (5.21)	96.8 (2.28)	95.3 (2.19)	96.5 (1.48)	95.1 (1.42)
0.5	0.5	0.5	96.9 (6.38)	95.4 (6.35)	96.2 (2.71)	95.3 (2.66)	95.9 (1.76)	95.1 (1.73)
0.7	0.3	0.7	96.0 (7.52)	95.5 (7.48)	95.5 (3.25)	95.3 (3.19)	95.6 (2.05)	95.1 (2.03)
0.8	0.2	0.8	95.8 (8.12)	95.5 (8.13)	95.5 (3.45)	95.2 (3.44)	95.4 (2.19)	95.1 (2.18)
0.95	0.05	0.95	95.4 (9.01)	95.6 (9.08)	95.3 (3.81)	95.3 (3.81)	95.1 (2.43)	95.2 (2.41)
*Cell entry is the actual coverage (the average value of the upper confidence limit on the log scale is in parentheses). Results based on 50,000 simulations. For all simulations, the natural log of the arithmetic mean is 0 in each simulation and there are ndays=3 at each site.

 

Table C-4 Part A -- Coverage (expressed as percentage) for nominal 95% confidence limits and average upper confidence limits for the two MOVER methods for strategy 1 when natural log scale total variance equals 0.25 or 2, values that were used in Table C-1, and ln(arithmetic mean)=0.

σs2/ Total vari- ance	Total variance: (σs2+σ2d(s))=0.25				Total variance: (σs2+σ2d(s))=2
	3 sites		5 sites		3 sites		5 sites
	Meth. UCLM,U	Meth. UCLM	Meth. UCLM,U	Meth. UCLM	Meth. UCLM,U	Meth. UCLM	Meth. UCLM,U	Meth. UCLM
0	97.2 (0.95)*	95.1 (0.90)	96.3 (0.36)	94.6 (0.33)	98.6 (6.8)	95.6 (6.4)	97.8 (2.1)	94.4 (1.8)
0.2	96.6 (1.24)	95.1 (1.22)	95.6 (0.43)	94.4 (0.41)	98.1 (9.1)	95.6 (8.8)	97.4 (2.6)	95.0 (2.4)
0.3	96.4 (1.39)	95.0 (1.37)	95.5 (0.47)	94.8 (0.46)	97.9 (10.3)	95.8 (10.0)	97.0 (2.8)	95.1 (2.7)
0.5	95.8 (1.68)	95.1 (1.67)	95.2 (0.55)	94.7 (0.54)	97.2 (12.7)	95.6 (12.5)	96.3 (3.4)	95.0 (3.3)
0.7	95.6 (1.99)	95.2 (1.99)	95.0 (0.62)	94.7 (0.62)	96.5 (15.1)	95.6 (15.0)	95.7 (3.9)	95.3 (3.9)
0.8	95.5 (2.15)	95.5 (2.14)	94.7 (0.66)	94.6 (0.66)	95.8 (16.3)	95.5 (16.2)	95.3 (4.2)	95.3 (4.)
0.95	95.3 (2.37)	95.1 (2.38)	94.7 (0.72)	94.9 (0.72)	95.5 (18.1)	95.4 (18.1)	95.0 (4.7)	95.2 (4.7)
* Cell entry is the actual coverage (the average value of the upper confidence limit on the natural log scale is in parentheses). Results based on 50,000 simulations. There are ndays=3 at each site.

Table C-4 Part B -- Coverage (expressed as percentage) for nominal 95% confidence limits and average upper confidence limits for the two MOVER methods for strategy 1 when natural log scale total variance equals 3 or 4, values that were used in Table C-1, and ln(arithmetic mean)=0.

σs2/ Total vari- ance	Total variance: (σs2+σ2d(s))=3				Total variance: (σs2+σ2d(s))=4
	3 sites		5 sites		3 sites		5 sites
	Meth. UCLM,U	Meth. UCLM	Meth. UCLM,U	Meth. UCLM	Meth. UCLM,U	Meth. UCLM	Meth. UCLM,U	Meth. UCLM
0	98.7 (10.2)*	95.5 (9.5)	98.0 (3.1)	94.6 (2.6)	98.8 (17.1)	95.6 (15.8)	98.1 (5.1)	94.7 (4.2)
0.2	98.4 (13.5)	95.8 (13.2)	97.6 (3.8)	95.3 (3.5)	98.5 (22.6)	95.9 (21.9)	97.8 (6.2)	95.2 (5.6)
0.3	98.2 (15.4)	95.6 (14.9)	97.4 (4.1)	95.2 (3.9)	98.3 (25.5)	95.6 (24.9)	97.5 (6.8)	95.2 (6.4)
0.5	97.6 (18.8)	95.7 (18.8)	96.5 (4.9)	95.1 (4.8)	97.6 (31.1)	95.4 (30.7)	96.8 (8.1)	95.1 (7.9)
0.7	96.4 (22.5)	95.5 (22.3)	95.8 (5.8)	95.0 (5.7)	96.6 (37.1)	95.4 (37.4)	95.5 (9.4)	95.1 (9.4)
0.8	95.8 (24.2)	95.4 (24.3)	95.6 (6.2)	95.2 (6.2)	95.9 (40.2)	95.4 (40.4)	95.3 (10.3)	95.2 (10.3)
0.95	95.3 (26.9)	95.5 (26.9)	95.2 (6.9)	95.1 (6.9)	95.2 (44.9)	95.0 (44.7)	95.2 (11.4)	95.0 (11.4)
* Cell entry is the actual coverage (the average value of the upper confidence limit on the natural log scale is in parentheses). Results based on 50,000 simulations. There are ndays=3 at each site.

In Tables C-3 and C-4, the upper confidence limits for the 5 site results for the ratio σ²_s/(σ²_s+σ²_d(s))=0.95, should approximate those from Table C-1, for the corresponding total variances. All of these tables are for arithmetic mean 1 (0 on log scale.) It makes sense to use results for this variance from Table C-4 because for this situation the total variance is most like that in Table C-2 with one dominant component. They do agree approximately. For instance, for total variance 0.25, Table C-4 gives an upper confidence limit for both methods of about 0.72, compared with 0.75 for method 2 in Table C-1. Coverage is about 95% from both these tables.

The coverage results in Tables C-3 and C-4, for variances between 0.25 and 5 indicate that the modified version of the MOVER (method 2, UCL_M) gives coverage much closer to the nominal 95% than the original version (method 1, UCL_M,U). The modified MOVER (method 2) is slightly anti-conservative for 5 sites and total variance 0.25. The coverages for the method 2 are never lower than 94.4% and never higher than 95.9%.

Statistical simulation was also used to evaluate the power of the modified MOVER for parameter values in the range from past studies, analogous to results in Table C-2. The results are shown in Tables C-5 and C-6. All calculations use n_days =3 at each site. The GMs considered in Table C-5 are 0.006, 0.01, and 0.025 mg/m³ (all less than the NIOSH REL). The GSD 1.92 is used because for several previous studies the total GSDs were between about 1.75 and 1.9. For instance, for σ²_s=0.106 and σ²_d(s)=0.319 (values from Table C-5) the total GSD is exp([0.106+0.319 ]^0.5)~1.92. The 0.025 mg/m³ GM was added to see how large the GM can be and still have sizable power. In addition, in order to study the power further, Table C-6 gives additional power results for five other total GSDs used in Table C-2, but only for GMs of 0.006 and 0.01 mg/m³. For the Tables C-5 and C-6, for each total GSD, the between- site variances shown are about 10%, 25%, 75% and 90% of the total variance.

Coverage is the fraction of simulations such that [ln(GM) + 0.5 (σ²_s+ σ²_d(s))] is less than the 95% upper confidence limit. Power is the fraction of simulations such that the upper confidence limit UCLM is less than the NIOSH REL of 0.05 mg/m³.

Table C-5: Coverage and power (expressed as percentages) for modified MOVER*

GM	Total GSD+	Be- tween site σ2s	With- in site σ2d(s)	3 sites		4 sites		5 sites
				Cvrg	Pwr	Cvrg	Pwr	Cvrg	Pwr
0.006	1.92	0.0426	0.383	95.3	67.1	94.9	93.8	94.8	99.5
0.006	1.92	0.106	0.319	95.4	59.2	94.9	88.4	94.8	98.2
0.006	1.92	0.319	0.106	95.4	42.5	95.2	71.3	94.9	88.2
0.006	1.92	0.383	0.0426	95.4	39.0	95.0	66.4	95.0	84.7
0.01	1.92	0.0426	0.383	95.3	54.8	95.0	84.6	94.6	96.4
0.01	1.92	0.106	0.319	95.4	47.6	94.9	77.0	94.8	92.4
0.01	1.92	0.319	0.106	95.4	33.4	95.1	56.3	94.8	75.1
0.01	1.92	0.383	0.0426	95.4	30.7	95.1	51.8	94.9	70.3
0.025	1.92	0.0426	0.383	95.4	22.6	94.9	35.0	94.7	47.9
0.025	1.92	0.106	0.319	95.4	19.4	95.0	30.2	94.7	40.7
0.025	1.92	0.319	0.106	95.4	14.0	95.1	20.6	94.8	27.0
0.025	1.92	0.383	0.0426	95.3	13.1	95.1	18.5	95.0	24.4
* For all simulations, there are ndays=3 days at each site. Results are based on 50,000 simulations. + Total GSD = ep, where p=(σ2s+σ2d(s))0.5

Table C-6 Part A: Coverage and power (expressed as percentages) for strategy 1 data. Simulation results are shown for GM=0.006 mg/m³, and for all total GSDs used in Table C-2 ; 50,000 simulations for each set of parameters

Total GSD+	Approx. Ratio σ2s /Total Variance	Be- tween site σ2s	With- in site σ2d(s)	GM=0.006 mg/m3
				3 sites		4 sites		5 sites
				Cvrg	Pwr	Cvrg	Pwr	Cvrg	Pwr
1.4	0.10	0.011	0.099	95.1	98.9	94.6	100.0	94.5	100.0
1.4	0.25	0.028	0.083	94.9	97.3	94.6	100.0	94.7	100.0
1.4	0.75	0.083	0.028	94.8	88.6	94.8	99.8	94.7	100.0
1.4	0.90	0.099	0.011	95.2	86.0	94.9	99.5	94.6	100.0
1.75	0.10	0.03	0.28	95.3	78.5	94.6	98.4	94.7	100.0
1.75	0.25	0.078	0.23	95.3	71.3	95.0	95.9	94.6	99.7
1.75	0.75	0.23	0.078	95.5	53.4	95.1	83.8	95.1	96.4
1.75	0.90	0.28	0.03	95.4	49.3	95.2	79.7	94.7	94.4
1.92	0.10	0.0426	0.383	95.3	67.1	94.9	93.8	94.8	99.5
1.92	0.25	0.106	0.319	95.4	59.2	94.9	88.4	94.8	98.2
1.92	0.75	0.319	0.106	95.4	42.5	95.2	71.3	94.9	88.2
1.92	0.90	0.383	0.0426	95.4	39.0	95.0	66.4	95.0	84.7
2.25	0.10	0.066	0.59	95.5	49.3	94.8	79.4	94.7	93.8
2.25	0.25	0.166	0.495	95.5	42.7	95.0	70.5	94.9	88.5
2.25	0.75	0.495	0.166	95.4	30.2	95.1	50.5	95.0	68.8
2.25	0.90	0.59	0.066	95.3	28.1	95.3	46.2	95.0	64.2
3.0	0.10	0.12	1.09	95.8	28.5	95.1	47.7	95.0	64.6
3.0	0.25	0.30	0.91	95.5	24.2	95.4	39.9	95.2	55.5
3.0	0.75	0.91	0.30	95.6	17.2	95.3	26.5	95.3	36.9
3.0	0.90	1.09	0.12	96.0	15.8	95.2	24.5	95.1	33.3
+ Total GSD = ep, where p=(σ2s+σ2d(s))0.5 Conclusions concerning coverage are that it is between 94.5% and 96.0%.

 

Table C-6 Part B: Coverage and power (expressed as percentages) for strategy 1 data. Simulation results are shown for GM=0.01 mg/m³, and for all total GSDs used in Table C-2 ; 50,000 simulations for each set of parameters

Total GSD+	Approx. Ratio σ2s /Total Variance	Be- tween site σ2s	With- in site σ2d(s)	GM=0.01 mg/m3
				3 sites		4 sites		5 sites
				Cvrg	Pwr	Cvrg	Pwr	Cvrg	Pwr
1.4	0.10	0.011	0.099	94.9	96.3	94.6	100.0	94.5	100.0
1.4	0.25	0.028	0.083	94.7	93.0	94.7	99.9	94.6	100.0
1.4	0.75	0.083	0.028	95.1	80.1	94.9	98.7	94.8	100.0
1.4	0.90	0.099	0.011	95.2	76.1	94.7	97.8	94.6	99.9
1.75	0.10	0.03	0.28	95.3	67.4	94.9	94.0	94.7	99.4
1.75	0.25	0.078	0.23	95.2	59.9	94.8	88.9	94.7	98.2
1.75	0.75	0.23	0.078	95.3	43.1	95.2	71.4	94.9	88.5
1.75	0.90	0.28	0.03	95.3	39.9	95.0	66.3	94.8	84.8
1.92	0.10	0.0426	0.383	95.3	54.8	95.0	84.6	94.6	96.4
1.92	0.25	0.106	0.319	95.4	47.6	94.9	77.0	94.8	92.4
1.92	0.75	0.319	0.106	95.4	33.4	95.1	56.3	94.8	75.1
1.92	0.90	0.383	0.0426	95.4	30.7	95.1	51.8	94.9	70.3
2.25	0.10	0.066	0.59	95.4	38.3	95.0	63.6	94.8	82.5
2.25	0.25	0.166	0.495	95.6	32.5	95.2	54.6	94.9	73.5
2.25	0.75	0.495	0.166	95.2	23.1	95.0	37.0	94.9	52.1
2.25	0.90	0.59	0.066	95.6	21.4	95.1	34.2	95.1	47.2
3.0	0.10	0.12	1.09	95.4	19.9	95.2	32.0	94.8	44.5
3.0	0.25	0.30	0.91	95.6	17.6	95.3	27.2	95.0	37.1
3.0	0.75	0.91	0.30	95.5	12.6	95.2	18.5	95.3	23.9
3.0	0.90	1.09	0.12	95.3	12.2	95.4	16.8	95.2	21.7
+ Total GSD = ep, where p=(σ2s+σ2d(s))0.5 Conclusions concerning coverage are that it is between 94.5% and 96.0%.

Conclusions concerning power from these two tables are:

1. It is useful to compare the power for five sites in Table C-5 (or C-6) to that in Table C-2 for GSD=1.92 and GM=0.006 mg/m³. For Table C-2, the power is about 82%, compared to about 85% from Table C-5 for =0.383 and =0.0426. When all the variance in the two component model is due to between-site variance, this is the same as the one component model, since the degrees of freedom for sites are the same. Likewise, for Table C-2, for five sites and GSD=3.0 power is about 31.4%, which is close to 33.3% from Table C-6 for =1.09 and GM=0.006 mg/m³. For both Tables C-5 and C-6, for each sample size and total GSD, the power decreases as the between-site variance becomes a larger portion of the total variance.
2. For the two lowest GMs shown (0.006 and 0.01 mg/m³) in Table C-5 or C-6, GSD=1.92, the highest power for the 3 site data (67.1% for GM=0.006 mg/m³ and 54.8% for GM=0.01 mg/m³) is approximately the same as the lowest power for the 4 site data (66.4% for GM=0.006 mg/m³ and 51.8% for GM=0.01 mg/m³). Thus, there is a big difference in power between sampling at 3 or at 4 sites for total GSD 1.92. Examination of Table C-6 indicates similar results for other total GSDs, especially at the 0.006 mg/m³ level.
3. If the GSD becomes much larger than 1.9, the power decreases considerably. This happens for both strategy 1 and strategy 2 designs. For the seven site strategy 2 design and GSD of 3.0 and GM of 0.006 mg/m³, the power is less than 50% (Table C-2). For the 5 site strategy 1 design with total GSD 3.0 and between variance accounting for at least 75% of the total variance and GM 0.006 mg/m³, the power is less than 40% (Table C-6). Thus, the discussion of power in this document relies considerably on observing total GSD much less than 3.
4. When the GM is 0.025 mg/m³, in Table C-5, for no sample size (≤5 sites) is the power greater than 50%.

Sampling Strategy 1 – Unbalanced Design

Although the recommendation for strategy 1 is to sample three days at each site, there will probably be studies where that is not possible. For such unbalanced data, the same formula for the UCL can be used; however, the following modifications must be made:

1. df2 = number of measurements-number of sites.
2. astd²_ws is the sum of the weighted within-site variances divided by df2. Each weight is the number of days at the site minus 1.
3. In equation (B-1), (n_{days - 1})/(n_days) is replaced by (1-nbar), where nbar is the average of the reciprocals of the number of days at the sites. Note that in the case of balanced data with n_days at each site, nbar is equal to 1/n_days and (1-nbar) reverts back to (n_{days - 1})/(n_days).
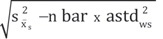4. =standard deviation between sites; note that for balanced data, nbar=1/n_days.

For unbalanced data, , the mean of site means on the natural log scale, is not statistically independent of and simulations are done to allow for this. Also, astd²_ws is statistically independent of both and and is generated that way in the simulations. Although there is some correlation of the estimators, Equation B-1 does not include any term for it. The simulations indicate that the coverage is acceptable. [Krishnamoorthy 2014] also does not include a term for the correlation of and . Note that and still denote the natural log scale mean of site means and the standard deviation of site means, respectively.

Statistical simulation was used to estimate coverage for several unbalanced designs based on 3 sites and (up to) 3 days per site. For these simulations, the population mean μ was set to -0.5(σ²_s + σ_(s)). Thus, for each choice of variances, the upper confidence limit is for exp[μ+0.5 ×(σ²_s + σ²_d(s) )]=exp(0)=1, or, equivalently, 0 on the natural log scale, as was also done in Tables C-3 and C-4. By making the arithmetic means the same, the upper confidence limits can be compared for different variance values. For each of the variance settings, 50,000 simulations were performed. The coverage is the percentage of simulations for which the arithmetic mean is less than the upper confidence limit. Only the modified MOVER method, UCL_M, results are shown in Table C-7.

 

Table C-7, Part A: Coverage (expressed as percentage of simulations) of the modified MOVER method for the unbalanced design based on 3 sites.

		Number of days at each site with k=3 sites:
σ2s	σ2d(s)	(3,3,3)	(3,3,2)	(3,2,2)	(3,3,1)
0	1	95.5 (3.27)*	95.5 (3.77)	95.5 (4.26)	95.5 (5.27)
0.2	0.8	95.5 (4.47)	95.5 (4.87)	95.5 (5.29)	95.5 (6.10)
0.3	0.7	95.5 (5.12)	95.4 (5.38)	95.5 (5.83)	95.5 (6.55)
0.5	0.5	95.4 (6.35)	95.4 (6.57)	95.6 (6.84)	95.5 (7.38)
0.7	0.3	95.5 (7.48)	95.5 (7.69)	95.6 (7.91)	95.6 (8.16)
0.8	0.2	95.5 (8.13)	95.5 (8.23)	95.5 (8.41)	95.5 (8.57)
0.95	0.05	95.6 (9.08)	95.5 (9.19)	95.4 (9.14)	95.6 (9.24)
*Cell entry is the actual coverage (the average value of the upper confidence limit on the natural log scale is in parentheses). Results based on 50,000 simulations.

 

Table C-7, Part B: Coverage (expressed as percentage of simulations) of the modified MOVER method for the unbalanced design based on 5 sites.

		Number of days at each site with k=5 sites:
σ2s	σ2d(s)	(3,3,3,3,3)	(3,3,3,3,2)	(3,3,3,2,2)	(3,3,2,2,1)
0	1	94.5 (0.96)*	94.4 (1.03)	94.6 (1.11)	94.6 (1.41)
0.2	0.8	94.8 (1.26)	94.8 (1.33)	94.9 (1.39)	94.9 (1.64)
0.3	0.7	95.1 (1.42)	95.0 (1.47)	94.9 (1.53)	94.9 (1.73)
0.5	0.5	95.1 (1.73)	95.0 (1.75)	94.8 (1.79)	95.1 (1.96)
0.7	0.3	95.1 (2.03)	95.1 (2.05)	95.1 (2.08)	95.2 (2.17)
0.8	0.2	95.1 (2.18)	95.0 (2.21)	95.2 (2.22)	95.3 (2.28)
0.95	0.05	95.2 (2.41)	95.2 (2.43.)	95.2 (2.43)	95.1 (2.44)
*Cell entry is the actual coverage (the average value of the upper confidence limit on the natural log scale is in parentheses). Results based on 50,000 simulations.

For the range of sample sizes evaluated for three sites, the coverage is close to the nominal 95%, and never anti-conservative. For five sites, there is slightly less than 95% coverage at very low between-site variance. The coverage is never less than 94.4%.

The average values of the upper confidence limits tend to increase as the total number of measurements decrease from 9 to 8 to 7. However, with just one day at one site, the configuration (3,3,1) has higher average upper confidence limits than the configuration (3,2,2), although they both have seven days of sampling. Also, as the between-site variance increases the differences in the average upper confidence limits become smaller for these designs. For the 0.95 between-site variance there is almost no difference—all average upper confidence limits are between 9.08 and 9.24 for the three site data. When there is almost no day to day variability, the value of the confidence limit depends only on the between-site variance.

Other simulations have been done for different total variance. Table C-8 has analogous results to those in Table C-7 for total natural log scale variance 0.25 and 3.0, values that were also evaluated in Table C-4 for balanced data.

Table C-8, Part A: Coverage (expressed as percentage of simulations) of the modified MOVER method for the unbalanced design based on 3 sites. 10,000 simulations for each specification of parameter values+, except that 50,000 were used for the balanced data, as reproduced from Table C-7.

			Number of days at each site with k=3 sites
Total Variance	σ2s	σ2s/Total Variance	(3,3,3)	(3,3,2)	(3,2,2)	(3,3,1)
0.25	0	0	95.1 (0.90)*	95.2 (1.04)	95.0 (1.14)	95.4 (1.41)
	0.05	0.2	95.1 (1.22)	94.9 (1.33)	95.5 (1.42)	95.6 (1.63)
	0.075	0.3	95.0 (1.37)	94.9 (1.43)	95.3 (1.56)	95.4 (1.73)
	0.125	0.5	95.1 (1.67)	95.6 (1.72)	95.2 (1.82)	95.1 (1.94)
	0.175	0.7	95.2 (1.99)	95.5 (2.02)	95.4 (2.08)	95.3 (2.16)
	0.2	0.8	95.5 (2.14)	95.6 (2.19)	95.2 (2.19)	94.9 (2.24)
	0.238	0.95	95.1 (2.38)	94.8 (2.35)	95.5 (2.36)	95.4 (2.41)
3.0	0	0	95.5 (9.52)	95.6 (11.08)	95.5 (12.46)	95.2 (15.50)
	0.6	0.2	95.8 (13.17)	95.8 (14.38)	95.5 (15.37)	95.8 (18.16)
	0.9	0.3	95.6 (14.87)	95.4 (16.17)	95.5 (17.41)	95.4 (19.15)
	1.5	0.5	95.7 (18.81)	95.5 (19.54)	95.7 (20.18)	95.6 (21.55)
	2.1	0.7	95.5 (22.31)	95.5 (22.79)	95.4 (23.56)	95.4 (24.18)
	2.4	0.8	95.4 (24.27)	95.6 (24.80)	95.6 (24.99)	95.5 (25.65)
	2.85	0.95	95.5 (26.92)	95.9 (26.95)	95.6 (27.56)	95.4 (27.33)
+There are relatively small differences between the simulation results for 10,000 and 50,000 simulations. Also, they are intended mainly to see if there is consistency with the 50,000 simulation results in Tables C-4 and C-7. *Cell entry is the actual coverage (the average value of the upper confidence limit on the natural log scale is in parentheses).

 

Table C-8, Part B: Coverage (expressed as percentage of simulations) of the modified MOVER method for the unbalanced design based on 5 sites. 10,000 simulations for each specification of parameter values+, except that 50,000 were used for the balanced data, as reproduced from Table C-7.

			Number of days at each site with k=5 sites
Total Variance	σ2s	σ2s/Total Variance	(3,3,3,3,3)	(3,3,3,3,2)	(3,3,3,2,2)	(3,3,2,2,1)
0.25	0	0	94.6 (0.33)*	94.2 (0.35)	94.8 (0.38)	94.7 (0.46)
	0.05	0.2	94.4 (0.41)	94.9 (0.43)	94.4 (0.44)	94.6 (0.51)
	0.075	0.3	94.8 (0.46)	94.6 (0.47)	94.6 (0.48)	94.8 (0.54)
	0.125	0.5	94.7 (0.54)	94.8 (0.55)	94.5 (0.56)	94.7 (0.60)
	0.175	0.7	94.7 (0.62)	94.7 (0.63)	94.6 (0.64)	94.7 (0.66)
	0.2	0.8	94.6 (0.66)	95.1 (0.67)	94.5 (0.66)	94.7 (0.68)
	0.238	0.95	94.9 (0.72)	94.5(0.72)	94.7 (0.72)	94.8 (0.73)
3.0	0	0	94.6 (2.58)	94.2 (2.78)	94.9 (3.00)	94.5 (3.92)
	0.6	0.2	95.3 (3.48)	95.3 (3.72)	95.1 (3.83)	95.3 (4.56)
	0.9	0.3	95.2 (3.92)	95.5 (4.10)	95.0 (4.23)	95.0 (4.93)
	1.5	0.5	95.1 (4.83)	95.5 (4.94)	95.5 (5.07)	95.1 (5.53)
	2.1	0.7	95.0 (5.73)	95.0 (5.88)	95.1 (5.89)	95.1 (6.21)
	2.4	0.8	95.2 (6.20)	95.1 (6.27)	95.2 (6.30)	95.2 (6.50)
	2.85	0.95	95.1 (6.86)	95.2 (6.93)	95.3 (7.01)	94.9 (6.96)
+There are relatively small differences between the simulation results for 10,000 and 50,000 simulations. Also, they are intended mainly to see if there is consistency with the 50,000 simulation results in Tables C-4 and C-7. *Cell entry is the actual coverage (the average value of the upper confidence limit on the natural log scale is in parentheses).

The results are similar to those in Table C-4 and C-7. For three sites, the coverage is always at least 95%, whereas for 5 sites at total variance 0.25, the coverage is a little less than 95%. The coverage is never less than 94.2%. For three or five sites, the average upper confidence limit increases as the total number of measurements decreases. This should result in some loss of statistical power. As in Table C-7, for the 0.95 ratio of between-site variance to total variance, there is almost no difference in expected values of the upper confidence limits, for the different designs at the given sample size and total variance.

References

Gibbons R, Coleman D [2001]. Statistical methods for detection and quantification of environmental contamination. Hoboken, NJ: John Wiley and Sons, Inc.

Krishnamoorthy K [2014]. A Simple Method for Assessing Occupational Exposure Via the One-Way Random Effects Model. Submitted to the Annals of Occupational Hygiene.

Krishnamoorthy K, and Mathew T [2002]. Assessing occupational exposure via the one-way random effects model with balanced data. Journal of Agricultural, Biological and Environmental Statistics. Vol. 7(3), p. 448.

Krishnamoorthy, K. and Peng, J. [2014]. Approximate One-Sided Tolerance Limits in Random Effects Models and Some Mixed Models and Comparisons. Journal of Statistical Simulation and Computation. Published online in March, 2014.

Land CE [1972]. An evaluation of approximate confidence interval estimation methods for lognormal means. Technometrics 14:145-158.

Mandel M [2013]. Simulation-based confidence intervals for functions with complicated derivatives. The American Statistician. 67(2), pp. 76.

NIOSH [2013a]. Control technology for crystalline silica exposure during pavement milling using a Roadtec milling machine equipped with a local exhaust ventilation system. By Hammond DR, Shulman SA Cincinnati, OH: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, EPHB Report No. 282-25a [http://www.cdc.gov/niosh/surveyreports/pdfs/282-25a.pdf].

NIOSH [2013b]. Control technology for crystalline silica exposure during pavement milling using a Wirtgen milling machine equipped with a vacuum cutting system. By Hammond DR, Shulman SA. Cincinnati, OH: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, EPHB Report No. 282-23a [http://www.cdc.gov/niosh/surveyreports/pdfs/282-23a.pdf].

Zou, G.Y., Taleban, J., and Huo, C.Y. [2009]. Confidence interval estimation for lognormal data with applications to health economics. Computational Statistics and Data Analysis. 53: pp. 3755-3764.

 

Appendix D: Use of the Spreadsheet

The Excel spreadsheet “mover_upper_confidence_limits.xlsx” is included with this document. It contains five worksheets: “Ex. Strategy 1-Balanced”, “Ex. Strategy 1-Unbalanced”, “Ex. Strategy 2”, “Blank Strategy 1”, and “Blank Strategy 2”. The first three of these worksheets have hypothetical example data that were discussed in Appendix B. The two worksheets “Blank Strategy 1” and “Blank Strategy 2” do not have data and should be used by manufacturers to input their data from field testing to calculate results. The user should choose these “blank” sheets according to the sampling strategy used, and enter the data in the red portion of the sheet. The upper confidence limit and other calculated estimates will then appear in bold at the bottom of the sheet on the right side. Whether the data for strategy 1 are balanced or unbalanced, the sheet “Blank Strategy 1” can be used. Whichever blank sheet is selected, that sheet should be copied elsewhere so that the blank sheet is available for new data.

 

Appendix E: Example Daily Dust Control Checklist

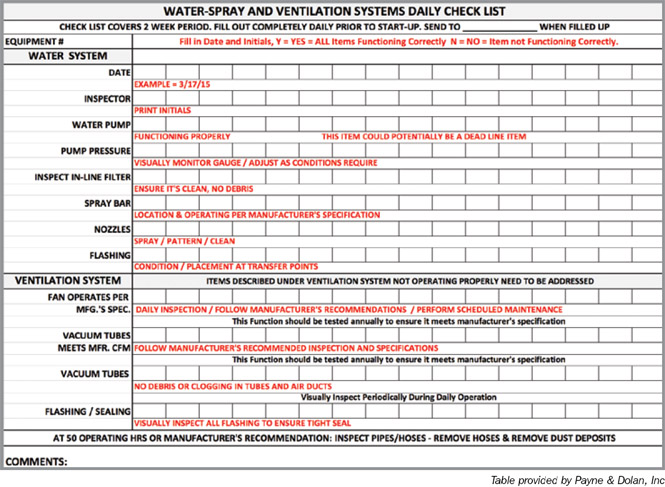
Appendix F: NAPA/AEM Best Practice Bulletin 1/12

 

Operational Guidance for Water Systems During Milling Operations

Best Practices Bulletin 1/12

www.asphaltpavement.org	www.aem.org

(Note: A PDF version of this Best Practive Bulletin is available at: http://store.aem.org/download/Milling-Water_Best%20Practices_01-12-12.pdf)

PROJECT PREPARATION

• Are there an adequate number of trained personnel for safe operation?
  • According to OSHA, each company needs to have a silica program to ensure that all employees have been trained in silica standards.
• Plan how water will be provided on the job site.
  • Ensure that water truck has enough capacity. Are permits and the proper hose and pumps on the job site?
• Know the work area. Insure work area is adequate to safely maneuver transport vehicle in work zone.
• Consider environmental conditions, such as freezing temperatures.
  • Possibly locate source for heated water or antifreeze for water tank.
• Ensure that the water filling points are accessible from the front and rear of the machine on narrow lane closures.
• Ensure that there are proper lighting and markers on the water truck for night operation.
• During winter months, make sure that the water system is winterized to ensure proper operations in cold weather and during shutdown overnight.
• If working at night, provide adequate lighting for safe operation. Have preparations been made to perform maintenance and inspections, and safely transfer water?

PRE-OPERATION INSPECTION

• Ensure that the mill has adequate water supply to begin operations.
• Check pump pressure to ensure that water pressure is set to manufacturer’s recommended specifications.
• Check individual spray bar locations to ensure that all nozzles are functioning correctly with a good spray pattern.
• Verify that all nozzles are functioning properly and spray pattern is correct for the designated location.

WARNING, TO AVOID INJURY:

• Read and understand manuals before operating.
• Keep hands clear of moving conveyor.
• Keep crew clear during machine movement.
• Stay away from cutter and discharge areas.
  
  

PREPARE FOR SAFE OPERATION

Before you begin to operate the machine, take time to check that it is in good working condition.

• Check and use all available protective and safety devices, such as railings, safety tread, handholds, and interlock devices.
• Perform daily and periodic service procedures as instructed by the equipment manufacturers.
• Check for broken, missing or damaged parts and loose or missing fasteners. Make any necessary repairs.
• Check that no warning tags have been placed on the machine.
• Check that warning signs, special instructions, and operator’s manuals are readable and in the proper location.
• Ensure all doors, safety devices, guards, and covers are in place and secured properly.

Operator training

• The operator must demonstrate a thorough understanding of the dust suppression systems on the machine:
  • Water system operation
    • Water application locations within the machine
    • Flow rates
    • Spray patterns
    • Anticipated water usage per unit time or per unit square yard.
    • Maintenance - ensure correct nozzles per manufacturer’s specifications.
    • Troubleshooting
    • Check in-line water filter
  • Visual inspection of seals, flashing, and enclosures, to ensure minimal dust leakage.

OPERATION

• Maintain clean water supply to the milling machine. Maintaining a clean water supply will reduce the chances of clogging strainers and nozzles.
• Monitor clean nozzles and water switch or flow control settings and system pressure to ensure proper application rate.
• Monitor conveyor belt speeds. Slow conveyer speed can cause material to stay in the housing longer, thereby reducing production and possible creating more airborne dust.
• Inspect and replace cutting tools (bits/teeth) as needed. Dull teeth reduce cutting efficiency, thereby reducing production and possibly creating more airborne dust.
• Front moldboard setting: lower front moldboard and / or primary conveyor to maximize housing exit window area. Reducing the exit window area will keep material in the housing longer, reducing production and creating more airborne dust.
• Make sure that the cutter drum kicker paddles are in good condition. Worn-out paddles will allow material to stay in the drum housing longer, reducing production and creating more airborne dust.
• Inspect the flashing that seals the conveyor frame to the belt. If worn and not replaced, dust / material exits the conveyor prematurely and can cause significant dust issues.

Safe operators know the work area and any potential hazards.

SAFETY RESOURCES

For cold planer Safety Manuals visit: http://shop.aem.org

 

Permission is granted to copy this bulletin, provided that it will be distributed without charge for educational purposes only, and that the bulletin is copied in its entirety, including this notice.

 

Appendix G: Glossary

Asphalt pavement milling machine: A milling machine or cold-planer is a type of highway construction machinery equipped with a toothed rotary cutter drum and conveyor system capable of rapid removal of recycled asphalt pavement.

Cutter drum: A rotary drum equipped with cutting teeth for removing recycled asphalt pavement.

Drum housing: The area inside the enclosure around the rotary cutter drum.

Ground person: The worker whose primary function is to operate the controls mounted to the sides of the machine at ground level.

Half-lane and larger milling machine: A half-lane cold planer that typically weighs more than 60,000 pounds and has a cutter drum width greater than 4 feet.

Operator: The worker whose primary function is to control the milling machine’s speed, direction, and conveyors.

Primary conveyor: The initial lift conveyor that transports recycled asphalt pavement from the cutter drum housing to the secondary conveyor.

Respirable crystalline silica: “That portion of airborne crystalline silica that is capable of entering the gas-exchange regions of the lungs if inhaled; by convention, a particle-size-selective fraction of the total airborne dust; includes particles with aerodynamic diameters less than approximately 10 μm and has a 50% deposition efficiency for particles with an aerodynamic diameter of approximately 4 μm” [NIOSH 2002].

Secondary conveyor: The longer conveyor that transports recycled asphalt pavement from the primary lift conveyor to a dump truck.

Reference

NIOSH [2002]. NIOSH hazard review: health effects of occupational exposure to respirable crystalline silica. Cincinnati, OH: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, DHHS (NIOSH) Publication No. 2002-129.

 

 

Delivering on the Nation’s promise: Safety and health at work for all people through research and prevention

To receive NIOSH documents or more information about occupational safety and health topics, contact NIOSH:

1–800–CDC–INFO (1–800–232–4636)
TTY: 1–888–232–6348
E-mail: cdcinfo@cdc.gov

or visit the NIOSH Web site at http://www.cdc.gov/niosh.

For a monthly update on news at NIOSH, subscribe to NIOSH eNews by visiting www.cdc.gov/niosh/eNews.

DHHS (NIOSH) Publication No. 2015–105